CheatSheet of Functions for Wolfram Mathematica

NOTE: Click on the Function name for usage examples!

$SetEpsilon=x

• Description: Sets the machine working precision to be used for numerical computations.
• Arguments: x is a positive double-precision variable.
• Comments: The default value is $MachineEpsilon as given by Mathematica. Once changed, it can be recovered to the default value by Clear[$SetEpsilon];.

$SetSignature={p,q,s}

• Description: Sets the indices (p,q,s) of the bilinear form used to define the Clifford Algebra (s is the degenerated index). It is assumed that for i>p+q+s we have GeometricProduct[e[i],e[i]]=0.
• Arguments: p, q, s are positive integer values.
• Comments: The default value is {20,0,0}. Once changed, it can be recovered to the default value by Clear[$SetSignature];.

Coeff[m,b]

• Description: Extracts the coefficient of the blade b in the multivector m.
• Arguments: b is a blade of grade and m is a multivector.

Dual[m,d]

• Description: Calculates the dual of the multivector m in .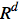
• Arguments: m is a multivector and d is a positive integer.

e[i]

• Description: e[i] is used to denote the i-th basis vector of .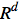
• Arguments: i is a integer greater than zero.

GADraw[m,v] ==Not implemented in version 0.7==

• Description: Plots a multivector m in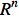 . To change the plot's view v, it must be used the ViewPoint function.
• Arguments: v can be omitted and the default value is ViewPoint->{0,1,0}.

GeometricCos[m,n]

• Description: Calculates the power series of the function Cos of the multivector m to a power n.
• Arguments: m is a multivector and n a positive integer.

GeometricExp[m,n]

• Description: Calculates the power series of the function Exp of the multivector m to a power n.
• Arguments: m is a multivector and n a positive integer.
• Comments: n can be omitted and the default value is 10.

GeometricPower[m,n]

• Description: Calculates the n-th power of the multivector m.
• Arguments: m is a multivector and n a positive integer.

GeometricProduct[m1,m2,...]

• Description: Calculates the geometric product of the multivectors m1,m2,....
• Arguments: m1,m2,... are multivectors.

GeometricProductSeries[sym,m,n]

• Description: Calculates the power series of the function sym of the multivector m to a power n.
• Arguments: sym is a Mathematica function, m is a multivector and n a positive integer.
• Comments: sym is any function which can be represented as a power series about zero. n can be omitted and the default value is 10.

GeometricSin[m,n]

• Description: Calculates the power series of the function Sin of the multivector m to a power n.
• Arguments: m is a multivector and n a positive integer.
• Comments: n can be omitted and the default value is 10.

GeometricTan[m,n]

• Description: Calculates the power series of the function Tan of the multivector m to a power n.
• Arguments: m is a multivector and n a positive integer.
• Comments: n can be omitted and the default value is 10.

Grade[m,r]

• Description: Extracts the term of grade r from the multivector m.
• Arguments: m is a multivector and r a positive integer.

i

• Description: Denotes the first complex component of a quaternion (see also j and k).
• Arguments: None.

Im[q]

• Description: Extracts the complex part of a quaternion q.
• Arguments: q is a quaternion.

InnerProduct[m1,m2,...]

• Description: Calculates the inner product of the multivectors m1,m2,....
• Arguments: m1,m2,... are multivectors.

j

• Description: Denotes the second complex component of a quaternion (see also i and k).
• Arguments: None.

k

• Description: Denotes the third complex component of a quaternion (see also i and j).
• Arguments: None.

Magnitude[m]

• Description: Calculates the magnitude of the multivector m.
• Arguments: m is a multivector.

MutivectorInverse[m]

• Description: Calculates (if it exists) the inverse of the multivector m.
• Arguments: m is a multivector.

OuterProduct[m1,m2,...]

• Description: Calculates the outer product of the multivectors m1,m2,....
• Arguments: m1,m2,... are multivectors.

Projection[v,b]

• Description: Projects the vector v onto the space spanned by the blade b.
• Arguments: v is a vector and b a r-blade.

Pseudoscalar[n]

• Description: Gives the pseudoscalar (volume element) of .
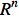• Arguments: n is a positive intger.

QuaternionConjugate[q]

• Description: Calculates the conjugate of the quaternion q.
• Arguments: q is a quaternion.

QuaternionInverse[q]

• Description: Calculates the inverse of the quaternion q.
• Arguments: q is a quaternion.

QuaternionMagnitude[q]

• Description: Calculates the magnitude of the quaternion q.
• Arguments: q is a quaternion.

QuaternionProduct[q1,q2,...]

• Description: Calculates the product of the quaternions q1,q2,....
• Arguments: q1,q2,... are quaternions.

Re[q]

• Description: Extracts the real part of the quaternion q.
• Arguments: q is a quaternion.

Reflection[v,w,x]

• Description: Calculates the specular reflection of the vector v by the plane spanned by the vectors w and x.
• Arguments: v, w and x are vectors.

Rejection[v,w,x]

• Description: Calculates the orthogonal projection of the vector v onto the orthogonal complement to the space spanned by the blade b.
• Arguments: v is a vector and b a r-blade.

Rotation[v,w,x,theta]

• Description: Rotates the vector v, by an angle theta. The plane spanned by w and x is left invariant.
• Arguments: v, w and x are vectors and theta is the rotation angle in degrees.
• Comments: theta can be omitted and in such case, the rotation angle is that formed by the vectors w and x.

ToBasis[v]

• Description: Transforms a vector from the Mathematica notation (list) to a linear combination of vectors e[i].
• Arguments: v is a vector given in Mathematica standard notation (list).

ToVector[v,d]

• Description: Transforms a vector from a linear combination of vectors or multivectors in the canonical form e[i] to the standard Mathematica notation (d-dimensional list).
• Arguments: v is a vector and d positive integer.
• Comments: d can be omitted and in such case the list dimension is the greatest dimension of the basis vectors e[i].

Turn[m]

• Description: Gives the reverse of the multivector m.
• Arguments: m is a multivector.