d3-force-reuse

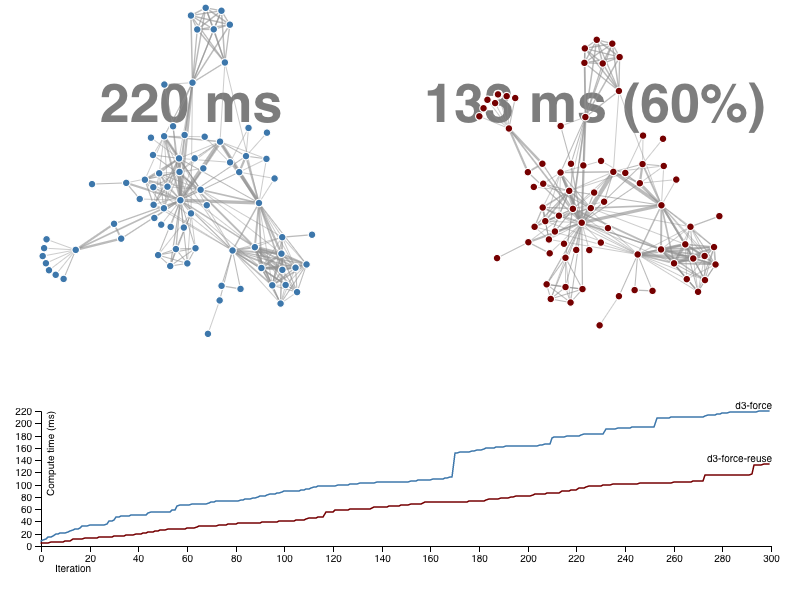
This module includes d3.forceManyBodyReuse(), a faster version of the repulsive force algorithm in d3-force. In practice, d3.forceManyBodyReuse() can decrease force-directed graph layout runtimes by 10% to 90% depending on the graph without a decrease in layout quality (as measured by graph layout quality metrics).

How does it achieve the performance speedup? The standard D3 algorithm uses the Barnes–Hut approximation to speed up the force calculations, which bases the force approximations on a quadtree that is recalculated after every tick of the layout algorithm. To reduce the runtime, d3.forceManyBodyReuse() only recalculates the quadtree once every 13 ticks. Experiments show that this is enough to achieve good quality graph layouts while still greatly speeding the algorithm.

This blog post discusses this in more detail, and the research paper contains the details of the algorithm experiments and their results. For a different approach to speeding up force layouts, see also d3-force-sampled.

If you use this module, please cite the following research paper:

Robert Gove. "It Pays to Be Lazy: Reusing Force Approximations to Compute Better Graph Layouts Faster." In Proceedings of the 11th Forum Media Technology (2018), pp. 43-51. Preprint PDF.

Credit

This module heavily uses code from d3-force. Many thanks to Mike Bostock for making this resource available open source!

Installing

If you use NPM, npm install d3-force-reuse. Otherwise, download the latest release. AMD, CommonJS, and vanilla environments are supported.

Usage

d3.forceManyBodyReuse() extends the d3.forceManyBody() API, and therefore can be used as a drop-in replacement for d3.forceManyBody(). The following is a simple example:

<script src="https://d3js.org/d3.v4.min.js"></script>
<script src="d3-force-reuse.js"></script>
<script>

var simulation = d3.forceSimulation(nodes)
  .force("link", d3.forceLink().id(function(d) { return d.id; }))
  .force("charge", d3.forceManyBodyReuse());

</script>

For full usage examples, see the simple example of d3-force-reuse or the d3-force-reuse speed comparison:

API Reference

Many-Body Reuse

The many-body (or n-body) force applies mutually amongst all nodes. It can be used to simulate gravity (attraction) if the strength is positive, or electrostatic charge (repulsion) if the strength is negative. This implementation uses quadtrees and the Barnes–Hut approximation to greatly improve performance; the accuracy can be customized using the theta parameter. In addition, the quadtree is only updated once every 13 ticks of the simulation. Research shows that this reduces running time while also preserving graph layout quality. The updating behavior can be controlled using the update parameter.

Unlike links, which only affect two linked nodes, the charge force is global: every node affects every other node, even if they are on disconnected subgraphs.

# d3.forceManyBodyReuse() <>

Creates a new many-body force with the default parameters.

# manyBodyReuse.update([update]) <>

If update is specified, sets the update function to the specified closure and returns this force. (A closure is a function that returns another function.) The outer function takes two parameters: the current iteration number i, which is a nonzero integer, and nodes, which is the array of nodes used by the many-body force simulation. The inner function returns true if a new quadtree should be calculated, and false otherwise. If update is not specified, returns the current closure, which defaults to following uniform distribution (i.e. evenly spaced intervals):

function () {
  return function (i, nodes) {
    if (i % 13 === 0) {
      return true;
    } else {
      return false;
    }
  };
}

To accelerate computation, this force only updates the quadtree used by the Barnes–Hut approximation once every 13 ticks of the simulation. Calculating the quadtree runs in O(n log n) time, so reducing the number of times the algorithm calculates a quadtree can greatly reduce the overall running time.

Note that update must be a closure, which allows the update function to maintain state. This allows users to specific update functions like the following, which updates the quadtree with decreasing frequency as the simulation progresses (although note that research shows the uniform function performs better):

var force = d3.forceManyBodyReuse().update(
  function () {
    var next = 1;
    return function (i, nodes) {
      var curr = Math.floor(4 * Math.log(i));
      if (curr !== next) {
        next = curr;
        return true;
      }
      return false;
    };
  }
)

# manyBodyReuse.strength([strength]) <>

If strength is specified, sets the strength accessor to the specified number or function, re-evaluates the strength accessor for each node, and returns this force. A positive value causes nodes to attract each other, similar to gravity, while a negative value causes nodes to repel each other, similar to electrostatic charge. If strength is not specified, returns the current strength accessor, which defaults to:

function strength() {
  return -30;
}

The strength accessor is invoked for each node in the simulation, being passed the node and its zero-based index. The resulting number is then stored internally, such that the strength of each node is only recomputed when the force is initialized or when this method is called with a new strength, and not on every application of the force.

# manyBodyReuse.theta([theta]) <>

If theta is specified, sets the Barnes–Hut approximation criterion to the specified number and returns this force. If theta is not specified, returns the current value, which defaults to 0.9.

To accelerate computation, this force implements the Barnes–Hut approximation which takes O(n log n) per application where n is the number of nodes. For each application, a quadtree stores the current node positions; then for each node, the combined force of all other nodes on the given node is computed. For a cluster of nodes that is far away, the charge force can be approximated by treating the cluster as a single, larger node. The theta parameter determines the accuracy of the approximation: if the ratio w / l of the width w of the quadtree cell to the distance l from the node to the cell’s center of mass is less than theta, all nodes in the given cell are treated as a single node rather than individually.

# manyBodyReuse.distanceMin([distance]) <>

If distance is specified, sets the minimum distance between nodes over which this force is considered. If distance is not specified, returns the current minimum distance, which defaults to 1. A minimum distance establishes an upper bound on the strength of the force between two nearby nodes, avoiding instability. In particular, it avoids an infinitely-strong force if two nodes are exactly coincident; in this case, the direction of the force is random.

# manyBodyReuse.distanceMax([distance]) <>

If distance is specified, sets the maximum distance between nodes over which this force is considered. If distance is not specified, returns the current maximum distance, which defaults to infinity. Specifying a finite maximum distance improves performance and produces a more localized layout.