Affine Cipher

Usage

The affine cipher is a type of monoalphabetic substitution cipher. It encrypts a text using an affine function (f(x) = ax + b).

Detailed Explanations : How it works?

1. Firstly, each character of the initial text (message to encrypt) is converted in a number from 0 to 25, corresponding to its position in the Latin alphabet which contains 26 letters --> (a = 0, b = 1 ... z = 25 ).

2. Then, each number obtained is transformed by an affine function (f(x) = ax + b). "x" is representing the number while "a" and "b" are defined during the encryption. "a" and "b" are the keys required to decrypt the final message.

3. If we take all the images and put them in a list, we obtain n numbers corresponding to n characters of the initial text. The next step consists in finding the values of modulo 26 of each number. (Modulo means remainder)

Example : Modulo 4 of 19 is 3 because 15 = 4 * 4 + 3 In the other hand, modulo 26 of 26 is 0 because 26 = 26 * 1 + 0

4. Therefore, we obtain a new list with n element, each between 0 and 25 both included. All these numbers are converted in letters of the Latin Alphabet using the tables below.

5. We finally create the final message by putting all the letters side by side.

Steps 1 and 4 can be done with these tables :

A	B	C	D	E	F	G	H	I	J	K	L	M
0	1	2	3	4	5	6	7	8	9	10	11	12

N	O	P	Q	R	S	T	U	V	W	X	Y	Z
13	14	15	16	17	18	19	20	21	22	23	24	25

Weaknesses

• As each letter is encrypted using the same function, trying many possibilities for a or b can be useful to decrypt the message. This is called the bruteforce method.

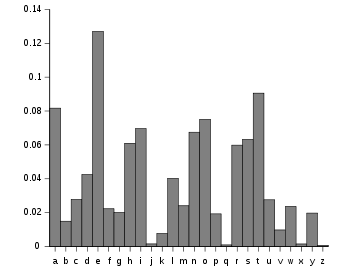
• We can also use frequency analysis if the message is long to decrypt the message as the most common letters in english are :

• Other possibilities include guessing the keys a and b.

• Knowing a can be helpful to eliminate a lot of solutions.

Example

Encrypting

• Message to encrypt : ATTACK
• Function used : f(x) = 3x + 6
• That means that a = 3 and b = 6

Using the above tables, ATTACK can be written as : 0 19 19 0 2 10 Images of each number :

• f(0) = 6
• f(19) = 63
• f(2) = 12
• f(10) = 36

The new list is : 6 63 63 6 12 36

Using the modulo 26 method, we obtain:

• Mod(6,26) = 6
• Mod(63,26) = 11
• Mod(12,26) = 12
• Mod(36,26) = 10

The final message is 6 11 11 6 12 10 and using the tables again, we convert them in the encrypted message :

GLLGMK

ATTACK is encrypted with the function 3x + 6 and becomes GLLGMK.

Decrypting

• Message to decrypt : GLLGMK
• That means that a = 3 and b = 6
• Hence a^-1 = modular multiplicative inverse of a modulo m (m = 26), a^-1 = 9
• Function used : f(x) = 9x - 54

Using the above tables, GLLGMK can be written as : 6 11 11 6 12 10 Images of each number :

• f(6) = 54 - 54 = 0
• f(11) = 99 - 54 = 45
• f(12) = 108 - 54 = 54
• f(10) = 90 - 54 = 36

The new list is : 0 45 45 0 54 36

Using the modulo 26 method, we obtain:

• Mod(0,26) = 0
• Mod(45,26) = 19
• Mod(54,26) = 2
• Mod(36,26) = 10

The final message is 0 19 19 0 2 10 and using the tables again, we convert them in the plain text :

ATTACK

GLLGMK is decrypted with the function f(x) = 3x + 6 and becomes ATTACK.