Website | Documentation | Tutorials | 中文文档 | Official Examples | Discussions

News

• 2022-12-28 -> v0.9.3 is now available! More datasets and operations of hypergraph are included!
• 2022-12-28 -> v0.9.3 正式发布！ 包含更多数据集和超图操作！
• 2022-09-25 -> v0.9.2 is now available! More datasets, SOTA models, and visualizations are included!
• 2022-09-25 -> v0.9.2 正式发布！ 包含更多数据集、最新模型和可视化功能！
• 2022-08-25 -> DHG's first version v0.9.1 is now available!
• 2022-08-25 -> DHG的第一个版本 v0.9.1 正式发布！

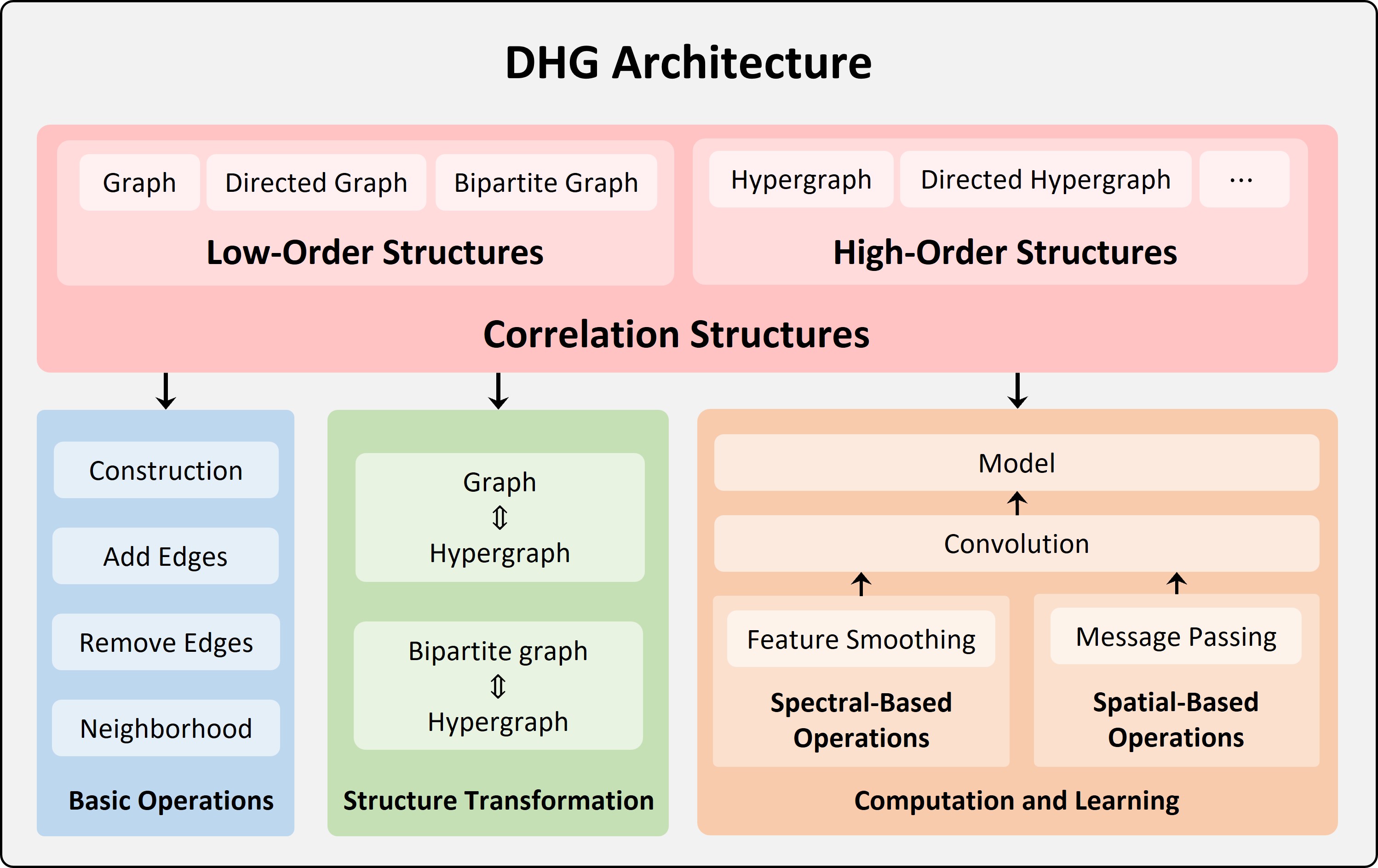
DHG (DeepHypergraph) is a deep learning library built upon PyTorch for learning with both Graph Neural Networks and Hypergraph Neural Networks. It is a general framework that supports both low-order and high-order message passing like from vertex to vertex, from vertex in one domain to vertex in another domain, from vertex to hyperedge, from hyperedge to vertex, from vertex set to vertex set.

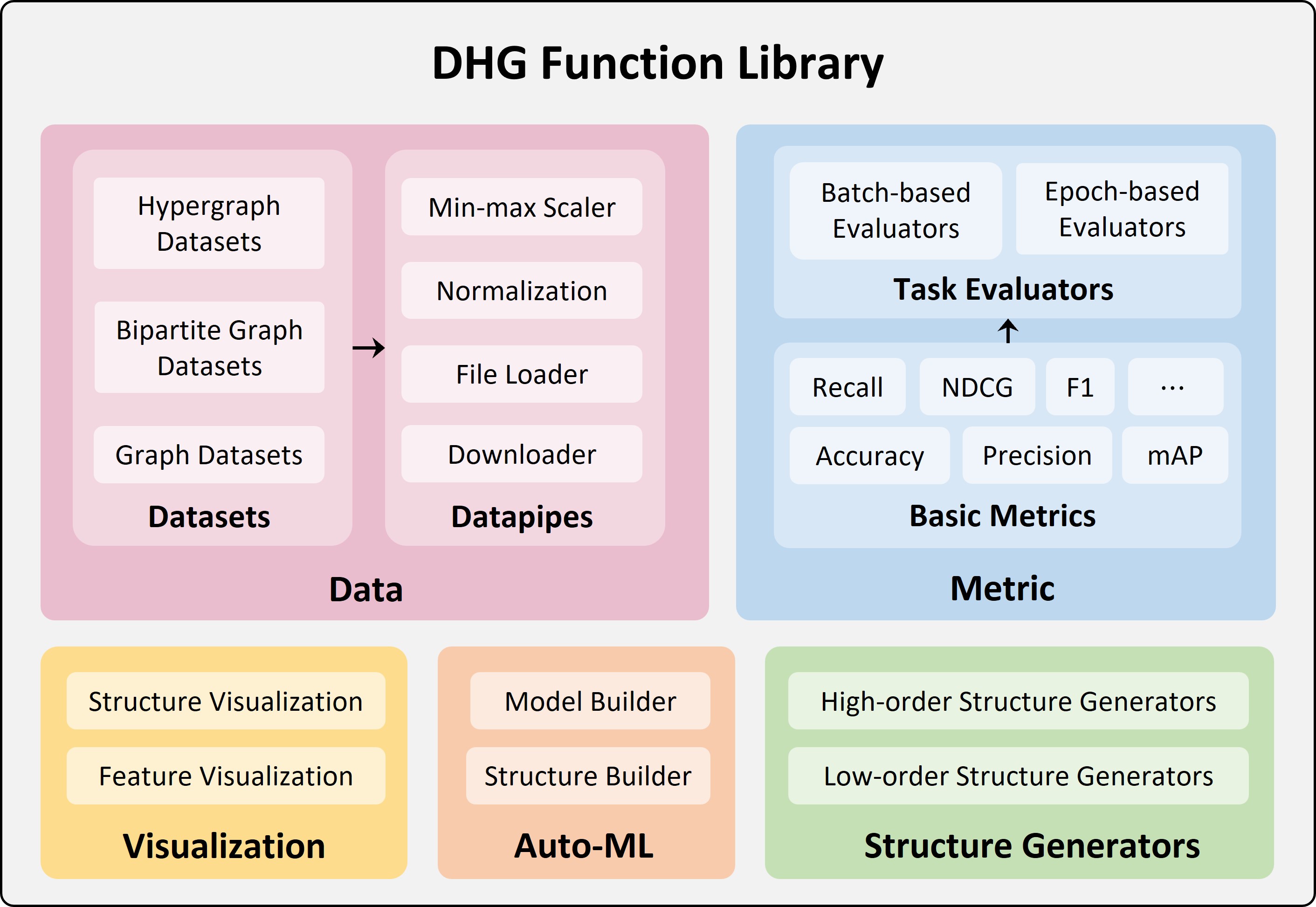
It supports a wide variety of structures like low-order structures (graph, directed graph, bipartite graph, etc.), high-order structures (hypergraph, etc.). Various spectral-based operations (like Laplacian-based smoothing) and spatial-based operations (like message psssing from domain to domain) are integrated inside different structures. It provides multiple common metrics for performance evaluation on different tasks. Many state-of-the-art models are implemented and can be easily used for research. We also provide various visualization tools for both low-order structures and high-order structures.

In addition, DHG's dhg.experiments module (that implements Auto-ML upon Optuna) can help you automatically tune the hyper-parameters of your models in training and easily outperforms the state-of-the-art models.

• Hightlights
• Installation
• Quick Start
• Examples
• Datasets
• Metrics
• Implemented Models

---

Highlights

• Support High-Order Message Passing on Structure: DHG supports pair-wise message passing on the graph structure and beyond-pair-wise message passing on the hypergraph structure.

• Shared Ecosystem with Pytorch Framework: DHG is built upon Pytorch, and any Pytorch-based models can be integrated into DHG. If you are familiar with Pytorch, you can easily use DHG.

• Powerful API for Designing GNNs and HGNNs: DHG provides various Laplacian matrices and message passing functions to help build your spectral/spatial-based models, respectively.

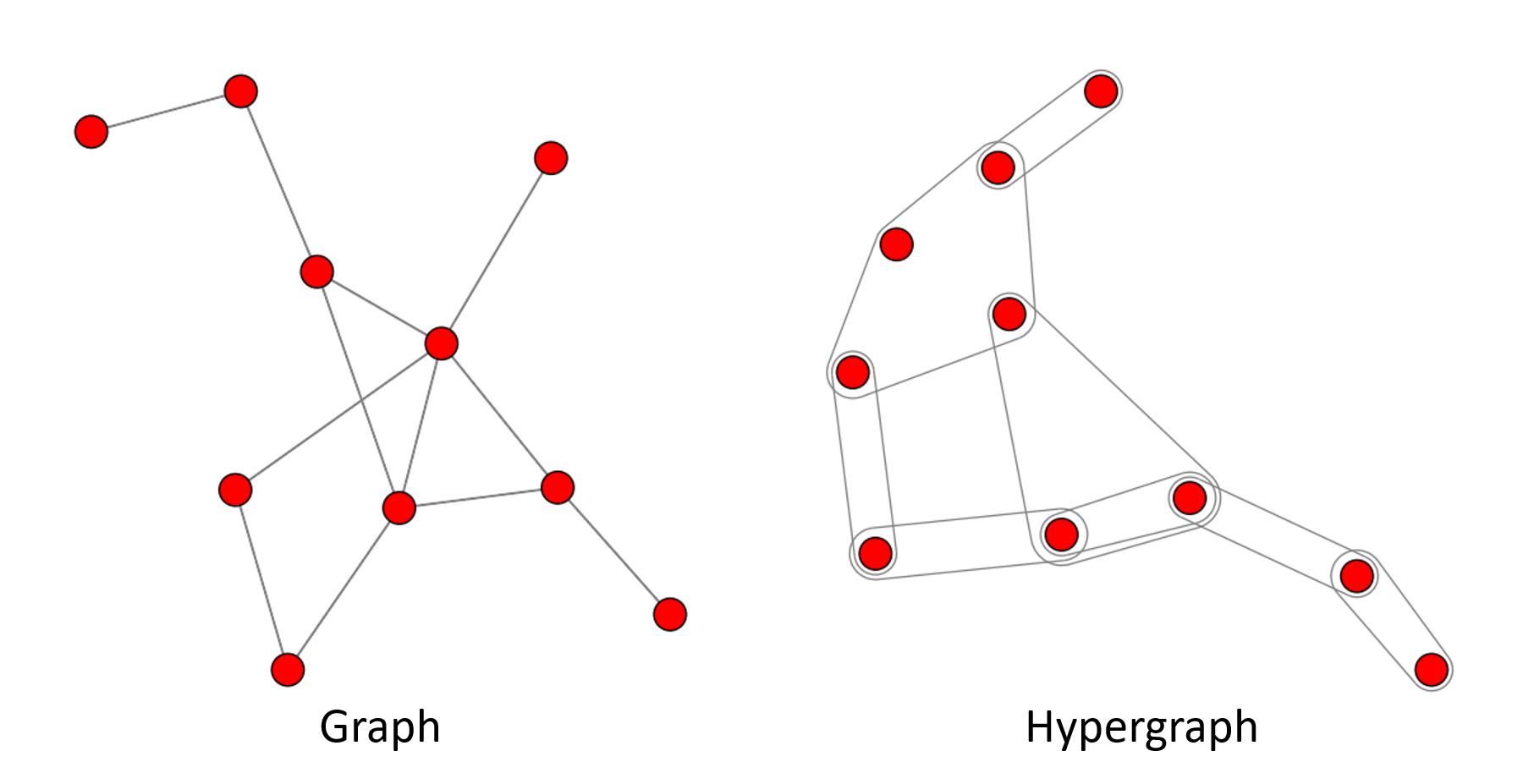
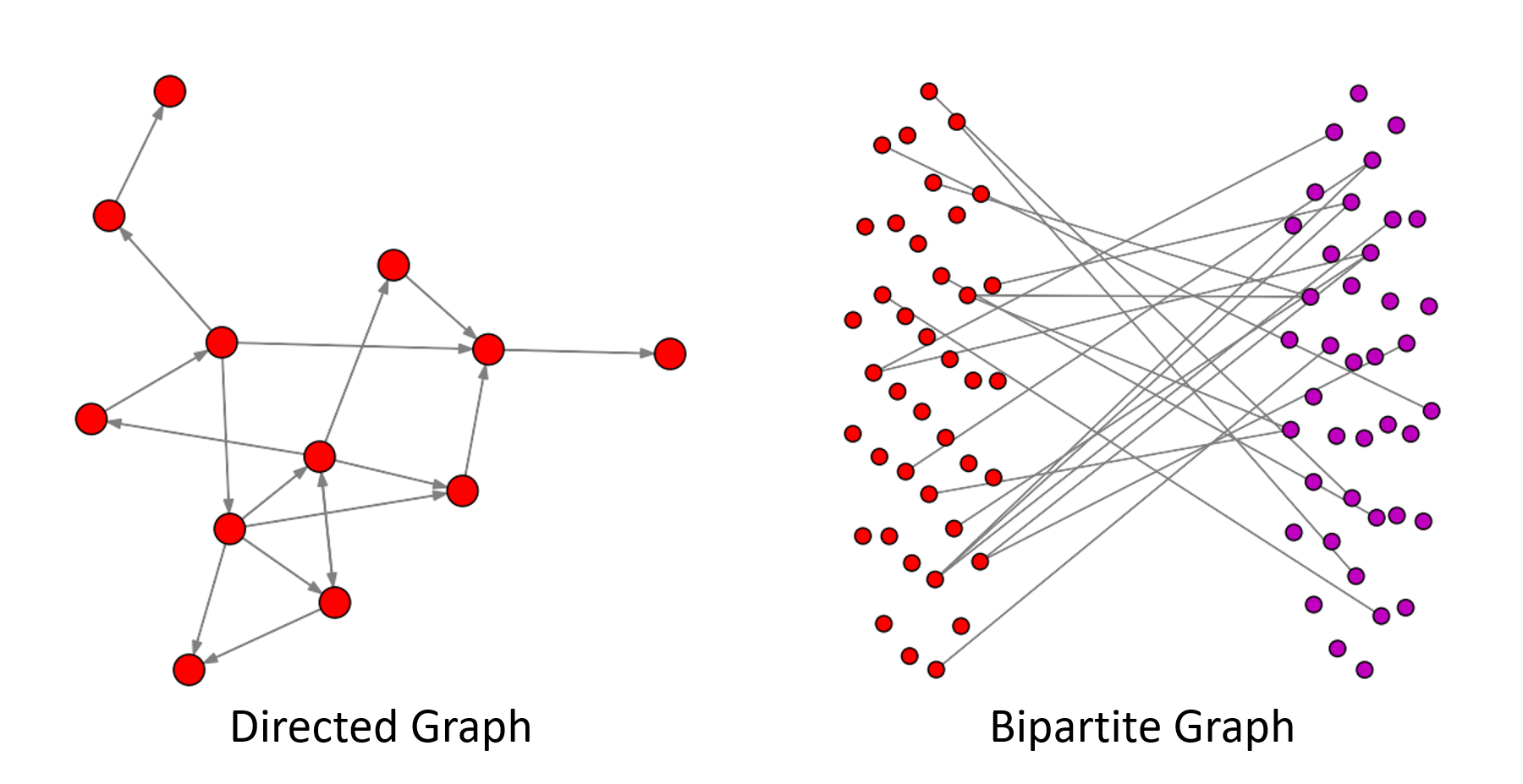
• Visualization of Graphs and Hypergraphs DHG provides a powerful visualization tool for graph and hypergraph. You can easily visualize the structure of your graph and hypergraph.

• Bridge the Gap between Graphs and Hypergraphs: DHG provides functions to build hypergraph from graph and build graph from hypergraph. Maybe promoting the graph to hypergraph can exploit those potential high-order connections and improve the performance of your model.

• Attach Spectral/Spatial-Based Operations to Structure: In DHG, those Laplacian matrices and message passing functions are attached to the graph/hypergraph structure. As soon as you build a structure with DHG, those functions will be ready to be used in the process of building your model.

• Comprehensive, Flexible, and Convenience: DHG provides random graph/hypergraph generators, various state-of-the-art graph/hypergraph convolutional layers and models, various public graph/hypergraph datasets, and various evaluation metrics.

• Support Tuning Structure and Model with Auto-ML: The Optuna library endows DHG with the Auto-ML ability. DHG supports automatically searching the optimal configurations for the construction of graph/hypergraph structure and the optimal hyper-parameters for your model and training.

Installation

Current, the stable version of DHG is 0.9.3. You can install it with pip as follows:

pip install dhg

You can also try the nightly version (0.9.4) of DHG library with pip as follows:

pip install git+https://github.com/iMoonLab/DeepHypergraph.git

Nightly version is the development version of DHG. It may include the lastest SOTA methods and datasets, but it can also be unstable and not fully tested. If you find any bugs, please report it to us in GitHub Issues.

Quick Start

Visualization

You can draw the graph, hypergraph, directed graph, and bipartite graph with DHG's visualization tool. More details see the Tutorial

import matplotlib.pyplot as plt
import dhg
# draw a graph
g = dhg.random.graph_Gnm(10, 12)
g.draw()
# draw a hypergraph
hg = dhg.random.hypergraph_Gnm(10, 8)
hg.draw()
# show figures
plt.show()

import matplotlib.pyplot as plt
import dhg
# draw a directed graph
g = dhg.random.digraph_Gnm(12, 18)
g.draw()
# draw a bipartite graph
g = dhg.random.bigraph_Gnm(30, 40, 20)
g.draw()
# show figures
plt.show()

Learning on Low-Order Structures

On graph structures, you can smooth a given vertex features with GCN's Laplacian matrix by:

import torch
import dhg
g = dhg.random.graph_Gnm(5, 8)
X = torch.rand(5, 2)
X_ = g.smoothing_with_GCN(X)

On graph structures, you can pass messages from vertex to vertex with mean aggregation by:

import torch
import dhg
g = dhg.random.graph_Gnm(5, 8)
X = torch.rand(5, 2)
X_ = g.v2v(X, aggr="mean")

On directed graph structures, you can pass messages from vertex to vertex with mean aggregation by:

import torch
import dhg
g = dhg.random.digraph_Gnm(5, 8)
X = torch.rand(5, 2)
X_ = g.v2v(X, aggr="mean")

On bipartite graph structures, you can smoothing vertex features with GCN's Laplacian matrix by:

import torch
import dhg
g = dhg.random.bigraph_Gnm(3, 5, 8)
X_u, X_v = torch.rand(3, 2), torch.rand(5, 2)
X = torch.cat([X_u, X_v], dim=0)
X_ = g.smoothing_with_GCN(X, aggr="mean")

On bipartite graph structures, you can pass messages from vertex in U set to vertex in V set by mean aggregation by:

import torch
import dhg
g = dhg.random.bigraph_Gnm(3, 5, 8)
X_u, X_v = torch.rand(3, 2), torch.rand(5, 2)
X_u_ = g.v2u(X_v, aggr="mean")
X_v_ = g.u2v(X_u, aggr="mean")

Learning on High-Order Structures

On hypergraph structures, you can smooth a given vertex features with HGNN's Laplacian matrix by:

import torch
import dhg
hg = dhg.random.hypergraph_Gnm(5, 4)
X = torch.rand(5, 2)
X_ = hg.smoothing_with_HGNN(X)

On hypergraph structures, you can pass messages from vertex to hyperedge with mean aggregation by:

import torch
import dhg
hg = dhg.random.hypergraph_Gnm(5, 4)
X = torch.rand(5, 2)
Y_ = hg.v2e(X, aggr="mean")

Then, you can pass messages from hyperedge to vertex with mean aggregation by:

X_ = hg.e2v(Y_, aggr="mean")

Or, you can pass messages from vertex set to vertex set with mean aggregation by:

X_ = hg.v2v(X, aggr="mean")

Examples

Building the Convolution Layer of GCN

class GCNConv(nn.Module):
    def __init__(self,):
        super().__init__()
        ...
        self.reset_parameters()

    def forward(self, X: torch.Tensor, g: dhg.Graph) -> torch.Tensor:
        # apply the trainable parameters ``theta`` to the input ``X``  
        X = self.theta(X)
        # smooth the input ``X`` with the GCN's Laplacian
        X = g.smoothing_with_GCN(X)
        X = F.relu(X)
        return X

Building the Convolution Layer of GAT

class GATConv(nn.Module):
    def __init__(self,):
        super().__init__()
        ...
        self.reset_parameters()

    def forward(self, X: torch.Tensor, g: dhg.Graph) -> torch.Tensor:
        # apply the trainable parameters ``theta`` to the input ``X``
        X = self.theta(X)
        # compute attention weights for each edge
        x_for_src = self.atten_src(X)
        x_for_dst = self.atten_dst(X)
        e_atten_score = x_for_src[g.e_src] + x_for_dst[g.e_dst]
        e_atten_score = F.leaky_relu(e_atten_score).squeeze()
        # apply ``e_atten_score`` to each edge in the graph ``g``, aggragete neighbor messages
        #  with ``softmax_then_sum``, and perform vertex->vertex message passing in graph 
        #  with message passing function ``v2v()``
        X = g.v2v(X, aggr="softmax_then_sum", e_weight=e_atten_score)
        X = F.elu(X)
        return X

Building the Convolution Layer of HGNN

class HGNNConv(nn.Module):
    def __init__(self,):
        super().__init__()
        ...
        self.reset_parameters()

    def forward(self, X: torch.Tensor, hg: dhg.Hypergraph) -> torch.Tensor:
        # apply the trainable parameters ``theta`` to the input ``X``
        X = self.theta(X)
        # smooth the input ``X`` with the HGNN's Laplacian
        X = hg.smoothing_with_HGNN(X)
        X = F.relu(X)
        return X

Building the Convolution Layer of HGNN $^+$

class HGNNPConv(nn.Module):
    def __init__(self,):
        super().__init__()
        ...
        self.reset_parameters()

    def forward(self, X: torch.Tensor, hg: dhg.Hypergraph) -> torch.Tensor:
        # apply the trainable parameters ``theta`` to the input ``X``
        X = self.theta(X)
        # perform vertex->hyperedge->vertex message passing in hypergraph
        #  with message passing function ``v2v``, which is the combination
        #  of message passing function ``v2e()`` and ``e2v()``
        X = hg.v2v(X, aggr="mean")
        X = F.relu(X)
        return X

Datasets

Currently, we have added the following datasets:

• Cora: A citation network dataset for vertex classification task.

• PubMed: A citation network dataset for vertex classification task.

• Citeseer: A citation network dataset for vertex classification task.

• BlogCatalog: A social network dataset for vertex classification task.

• Flickr: A social network dataset for vertex classification task.

• Github: A collaboration network dataset for vertex classification task.

• Facebook: A social network dataset for vertex classification task.

• MovieLens1M: A movie dataset for user-item recommendation task.

• AmazonBook: An Amazon dataset for user-item recommendation task.

• Yelp2018: A restaurant review dataset for user-item recommendation task.

• Gowalla: A location's feedback dataset for user-item recommendation task.

• TecentBiGraph: A social network dataset for vertex classification task.

• CoraBiGraph: A citation network dataset for vertex classification task.

• PubmedBiGraph: A citation network dataset for vertex classification task.

• CiteseerBiGraph: A citation network dataset for vertex classification task.

• Cooking200: A cooking recipe dataset for vertex classification task.

• CoauthorshipCora: A citation network dataset for vertex classification task.

• CoauthorshipDBLP: A citation network dataset for vertex classification task.

• CocitationCora: A citation network dataset for vertex classification task.

• CocitationPubmed: A citation network dataset for vertex classification task.

• CocitationCiteseer: A citation network dataset for vertex classification task.

• YelpRestaurant: A restaurant-review network dataset for vertex classification task.

• WalmartTrips: A user-product network dataset for vertex classification task.

• HouseCommittees: A committee network dataset for vertex classification task.

• News20: A newspaper network dataset for vertex classification task.

• DBLP8k: The DBLP-8k dataset is a citation network dataset for link prediction task.

Metrics

Classification Metrics

• Accuracy: Calculates the accuracy of the predictions.

• F1-Score: Calculates the F1-score of the predictions.

• Confusion Matrix: Calculates the confusion matrix of the predictions.

Recommender Metrics

• Precision@k: Calculates the precision@k of the predictions.

• Recall@k: Calculates the recall@k of the predictions.

• NDCG@k: Calculates the normalized discounted cumulative gain@k of the predictions.

Retrieval Metrics

• Precision@k: Calculates the precision@k of the predictions.

• Recall@k: Calculates the recall@k of the predictions.

• mAP@k: Calculates the mAP@k of the predictions.

• NDCG@k: Calculates the normalized Discounted Cumulative Gain@k of the predictions.

• mRR@k: Calculates the mean Reciprocal Rank@k of the predictions.

• PR-Curve: Calculates the precision-recall curve of the predictions.

Implemented Models

On Low-Order Structures

• GCN model of Semi-Supervised Classification with Graph Convolutional Networks paper (ICLR 2017).

• GraphSAGE model of Inductive Representation Learning on Large Graphs paper (NeurIPS 2017).

• GAT model of Graph Attention Networks paper (ICLR 2018).

• GIN model of How Powerful are Graph Neural Networks? paper (ICLR 2019).

• NGCF model of Neural Graph Collaborative Filtering paper (SIGIR 2019).

• LightGCN model of LightGCN: Lightweight Graph Convolutional Networks paper (SIGIR 2020).

• BGNN-Adv model of Cascade-BGNN: Toward Efficient Self-supervised Representation Learning on Large-scale Bipartite Graphs paper (TNNLS 2020).

• BGNN-MLP model of Cascade-BGNN: Toward Efficient Self-supervised Representation Learning on Large-scale Bipartite Graphs paper (TNNLS 2020).

On High-Order Structures

• HGNN model of Hypergraph Neural Networks paper (AAAI 2019).

• HGNN+ model of HGNN+: General Hypergraph Neural Networks paper (IEEE T-PAMI 2022).

• HyperGCN model of HyperGCN: A New Method of Training Graph Convolutional Networks on Hypergraphs paper (NeurIPS 2019).

• DHCF model of Dual Channel Hypergraph Collaborative Filtering paper (KDD 2020).

• HNHN model of HNHN: Hypergraph Networks with Hyperedge Neurons paper (ICML 2020).

• UniGCN model of UniGNN: a Unified Framework for Graph and Hypergraph Neural Networks paper (IJCAI 2021).

• UniGAT model of UniGNN: a Unified Framework for Graph and Hypergraph Neural Networks paper (IJCAI 2021).

• UniSAGE model of UniGNN: a Unified Framework for Graph and Hypergraph Neural Networks paper (IJCAI 2021).

• UniGIN model of UniGNN: a Unified Framework for Graph and Hypergraph Neural Networks paper (IJCAI 2021).

Citing

If you find DHG is useful in your research, please consider citing:

@article{gao2022hgnn,
  title={HGNN $\^{}+ $: General Hypergraph Neural Networks},
  author={Gao, Yue and Feng, Yifan and Ji, Shuyi and Ji, Rongrong},
  journal={IEEE Transactions on Pattern Analysis and Machine Intelligence},
  year={2022},
  publisher={IEEE}
}

@inproceedings{feng2019hypergraph,
  title={Hypergraph neural networks},
  author={Feng, Yifan and You, Haoxuan and Zhang, Zizhao and Ji, Rongrong and Gao, Yue},
  booktitle={Proceedings of the AAAI conference on artificial intelligence},
  volume={33},
  number={01},
  pages={3558--3565},
  year={2019}
}

The DHG Team

DHG is developed by DHG's core team including Yifan Feng, Xinwei Zhang, Jielong Yan, Shuyi Ji, Yue Gao, and Qionghai Dai. It is maintained by the iMoon-Lab, Tsinghua University. You can contact us at email.

License

DHG uses Apache License 2.0.