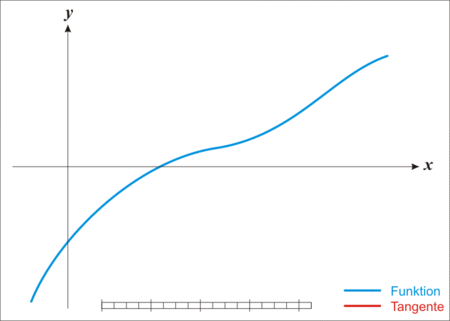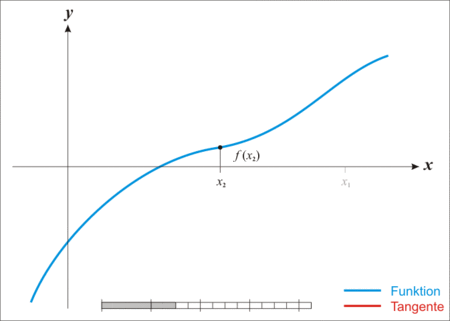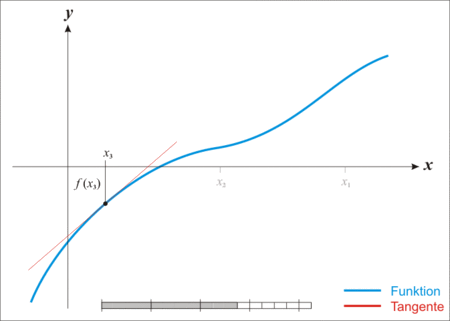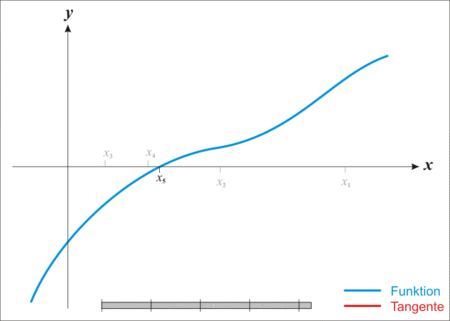
- pattern matching - различна имплементация в зависимост от стойността/формата на типа на определен аргумент.
- guards, where - като
condвscheme, връщаме резултата на първата булева истина. - let in - expression с локален скоуп на дефинираните в него променливи.
-
case ofexpressions expression с резултат зависещ от pattern match-ната стойност.case expression of pattern -> result pattern -> result pattern -> result ...
Пример
scaleVector :: Num a => [a] -> a -> [a] scaleVector v n = case v of [] -> [] (ah : at) -> ah * n : scaleVector at n
-
Ф-ята
zip- зипва елементи от 2 списъка Създава списък от двойки от елементите на 2та списъка по индекси. Приключва след като свърши по-краткият списък.> zip [1, 2, 3] [4, 5, 6, 7] [(1,4),(2,5),(3,6)]
-- file.hs
main = putStr "Hello world!"
> ghc file.hs
> ./fileДават ни начин да зададем специфично име на определен тип (може да се използва за задаване на семантично по-подходящи типове)
type Name = String
type StudentIdentifier = Int
type Vector = (Double, Double, Double)
type IntToInt = Int -> IntПолиморфни типови псевдоними
type Vector а = (а, а, а)
type Function a = a -> a
type BinaryFunction a b c = a -> b -> c
type Predicate a = a -> Bool-
$ е просто функция дефинирана по следния начин:
($) :: (a -> b) -> a -> b f $ x = f x
Трябва ли ни това, нали може да си викаме функции със
space.Нормалното викане на функции е с най висок приоритет и е ляво асоциативно, т.е.
f a b c == (((f a) b) c). Викането на ф-я с $ е дясно асоциативно.Вместо да пишем
factorial (n - 1)можем да напишемfactorial $ n - 1, т.е. спестяваме си скобите.Може да си мислим че когато сложим този оператор израза вдясно от него се загражда в скоби (от оператора до края на реда).
-
Композиция на функции (g ∘ f)
(.) :: (b -> c) -> (a -> b) -> a -> c f . g = \x -> f (g x)
Работи замо за едноаргументни функции.
Вместо
ghci> map (\x -> negate (abs x)) [5,-3,-6,7,-3,2,-19,24] [-5,-3,-6,-7,-3,-2,-19,-24]
пишем
ghci> map (negate . abs) [5,-3,-6,7,-3,2,-19,24] [-5,-3,-6,-7,-3,-2,-19,-24]
Още един пример откраднат от книгата
fn = ceiling . negate . tan . cos . max 50
Вижте функцията integrate за по-интересен пример с комбинация на 2те.
Това са функции които приемта други функции като аргументи и/или връщат функция.
-
Преди всичко -
mapиfilter.map- прилага функция върху елементите на лист.filter- филтрира елементите на лист с определен предикат.
-
🍛 Kъри - викаме функция, ама без всичите и параметри, тя връща ф-я с останалите параметри.
-
Space- оператор за извукване на ф-я. Викайки функция с няколко параметъра ние всъщност викаме последователно няколко функции. -
Частичното прилагане на параметри обяснява и синтаксиса на типовете на функците.
sum' :: Num a => a -> a -> a -> a sum' a b c = a + b + c sum3 :: Integer -> Integer -> Integer sum3 = sum' 3 sum5 :: Integer -> Integer sum5 = sum' 3 2 fifteen :: Integer fifteen = sum5 10
> :t sum' sum' :: Num a => a -> a -> a -> a
-
Къри на бинарни функции
(/) 10 2==(10/) 2==5.0/=(/10) 2biggerThan200 x = x > 200== (>200)
squares' :: [Integer] squares' = map (^ 2) [1 .. 30] biggerSquares' :: [Integer] biggerSquares' = filter (> 200) squares'
-
-
Удобно е за конструиране на по-специфични функции, които може да носят повече смисъл в някои ситуации.
takeFirstFive :: [a] -> [a] takeFirstFive = take 5
-
-
Каноничен пример за функция от по-висок ред
Кой математически оператор взима ф-я като аргумент и връща ф-я? Точно така
Производната.derive :: Fractional a => a -> (a -> a) -> a -> a derive eps f x = (f (x + eps) - f x) / eps df :: (Double -> Double) -> Double -> Double df = derive 1e-10 > df (^2) 2 4.000000330961484 > df sin 0 1.0 > df sin (pi / 2) 0.0 > df cos (pi / 2) -1.000000082740371
Да имплементираме оператор за интегриране:
integrate :: (Num a, Enum a) => a -> (a, a) -> (a -> a) -> a integrate eps (a, b) f = sum . map (* eps) . map f $ [a, a + eps .. b] (~∫) :: (Double, Double) -> (Double -> Double) -> Double (~∫) = integrate 1e-4 > (0, pi) ~∫ sin 1.999999997939027
Проверка - https://www.wolframalpha.com/input/?i=integrate+sin+x+dx+from+0+to+pi
- Напишете ф-я
lSystem axiom rules, която да връща безкраен списък от стрингове със следните свойства:
axiomе стринг.rulesе списък от наредени двойки(Char, [Char])- Всяки следващ стринг трябва да е получен чрез заместване на символите от предния стринг със стрингове от правилата.
- Първият стринг в безкрайният списък от състояния е аксиомата.
Пример:
axiom = 'A'
rules = [('A', "AB"), ('B', "A")]
last $ take 7 $ lSystem axiom rules
> ABAABABAABAABABAABABAABAABABAABAAB-
Напишете ф-я която да намира приближение на корените на функция по метода на Нютон.
-
Имплементирайте ф-я
quicksort lкоято да сортира елементите в даден списък. Quicksort WikipediaQuicksort has become a sort of poster child for Haskell. ...even though implementing quicksort in Haskell is considered really cheesy because everyone does it to showcase how elegant Haskell is.
-
Напишете функция
collatz n, която да пресмята редица на Колатз.-
редицата на Колатз за число n се пресмята като започнем от n и прилагаме итеративно следната трансформация:
Ако n e четно -> върни n / 2 Иначе -> върни 3 * n + 1-
редицата приключва когато стигем числото 1.
-
Пример
> collatz 25 [25,76,38,19,58,29,88,44,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1]
-
-
(***много повишена трудност) Бонус задачка - намерете редица на Kолатз която не завършва на 1. (напишете израз който търси отговора)
-