-
Notifications
You must be signed in to change notification settings - Fork 173
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Gradient calculation in paper #27
Comments
|
Please notice that The equation with red rectangle contains only one timestamp of full weights updating, so it shows the case of out-degrees of It is too complicate to show timestamps $t_{j}$s in a equation. If you want to add gradient information of |
|
thanks for your reply. @WongKinYiu |
|
@WongKinYiu Thanks very much for your patient reply. Good luck to you. |
1 similar comment
|
@WongKinYiu Thanks very much for your patient reply. Good luck to you. |
|
@WongKinYiu dear author ,i still dont understand why we should use g_{0} to update w1.In your discription, g_{0} equals to |

















Hi,
I am interested in CSPNet recently, and reading the paper: https://arxiv.org/pdf/1911.11929.pdf.
But I have a question about the gradient calculation in page 4, in the paper the gradient calculate as
Don't this part is calculated as this?
also I want to confirm that if the definition of gi is the partial differential of error to weight? that is,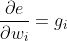
I was very confuse about this part, hope that you can help me.
The text was updated successfully, but these errors were encountered: