Skip to content

Latest commit

 

History

History
945 lines (695 loc) · 61.4 KB

Decsion tree and ensemble methods.md

File metadata and controls

945 lines (695 loc) · 61.4 KB
Raw

Tree-based Learning Algorithms

高效决策树算法系列笔记

The simple function is a real-valued function $f: \mathrm{X}\to \mathbb{R}$ if and only if it is a finite linear combination of characteristic functions: $$f=\sum_{i=1}^{n}a_k {\chi}{S{k}}$$ where $a_k\in\mathbb{R}$ and the characteristic function is defined as follow $${\chi}{S{k}}=\begin{cases}1, &\text{if $x \in S_{k}$}\ 0, &\text{otherwise}\end{cases}.$$

The tree-based learning algorithms take advantages of these universal approximators to fit the decision function.

The core problem is to find the optimal parameters $a_k\in\mathbb{R}$ and the region $S_k\in\mathbb{R}^p$ when only some finite sample or training data ${(\mathrm{x}_i, y_i)\mid i=1, 2, \dots, n}$ is accessible or available where $\mathrm{x}_i\in\mathbb{R}^p$ and $y_i\in\mathbb{R}$ or some categorical domain and the number of regions also depends on the training data set.

Decision Tree

In brief, A decision tree is a classifier expressed as a recursive partition of the instance space.

A decision tree is the function $T :\mathbb{R}^d \to \mathbb{R}$ resulting from a learning algorithm applied on training data lying in input space $\mathbb{R}^d$ , which always has the following form: $$ T(x) = \sum_{i\in\text{leaves}} g_i(x)\mathbb{I}(x\in R_i) = \sum_{i\in ,\text{leaves}} g_i(x) \prod_{a\in,\text{ancestors(i)}} \mathbb{I}(S_{a (x)}=c_{a,i}) $$ where $R_i \subset \mathbb{R}^d$ is the region associated with leaf ${i}$ of the tree, $\text{ancestors(i)}$ is the set of ancestors of leaf node i, $c_{a,i}$ is the child of node a on the path from a to leaf i, and $S_a$ is the n-array split function at node a. $g_i(\cdot)$ is the decision function associated with leaf i and is learned only from training examples in $R_i$.

The $g_{i}(x)$ can be a constant in $\mathbb{R}$ or some mathematical expression such as logistic regression. When $g_i(x)$ is constant, the decision tree is actually piecewise constant, a concrete example of simple function.

A decision tree is a set of questions(i.e. if-then sentence) organized in a hierarchical manner and represented graphically as a tree. It use 'divide-and-conquer' strategy recursively. It is easy to scale up to massive data set. The models are obtained by recursively partitioning the data space and fitting a simple prediction model within each partition. As a result, the partitioning can be represented graphically as a decision tree. Visual introduction to machine learning show an visual introduction to decision tree.

Algorithm Pseudocode for tree construction by exhaustive search

  1. Start at root node.
  2. For each node ${X}$, find the set ${S}$ that minimizes the sum of the node $\fbox{impurities}$ in the two child nodes and choose the split ${X^{\ast}\in S^{\ast}}$ that gives the minimum overall $X$ and $S$.
  3. If a stopping criterion is reached, exit. Otherwise, apply step 2 to each child node in turn.

Creating a binary decision tree is actually a process of dividing up the input space according to the sum of impurities.

This learning process is to minimize the impurities. C4.5 and CART6 are two later classification tree algorithms that follow this approach. C4.5 uses entropy for its impurity function, whereas CART uses a generalization of the binomial variance called the Gini index.

If the training set $D$ is divided into subsets $D_1,\dots,D_k$, the entropy may be reduced, and the amount of the reduction is the information gain,

$$ G(D; D_1, \dots, D_k)=Ent(D)-\sum_{i=1}^{k}\frac{|D_k|}{|D|}Ent(D_k) $$

where $Ent(D)$, the entropy of $D$, is defined as

$$ Ent(D)=\sum_{y \in Y} P(y|D)\log(\frac{1}{P(y | D)}). $$

The information gain ratio of features $A$ with respect of data set $D$ is defined as

$$ g_{R}(D,A)=\frac{G(D,A)}{Ent(D)}. $$ And another option of impurity is Gini index of probability $p$:

$$ Gini(p)=\sum_{y}p_y (1-p_y)=1-\sum_{y}p_y^2. $$

Algorithm Impurity
ID3 Information Gain
C4.5 Normalized information gain ratio
CART Gini Index

$\color{red}{\text{PS: all above impurities}}$ are based on the probability $\fbox{distribuion}$ of data.

Like other supervised algorithms, decision tree makes a trade-off between over-fitting and under-fitting and how to choose the hyper-parameters of decision tree such as the max depth? The regularization techniques in regression may not suit the tree algorithms such as LASSO.

Pruning is a regularization technique for tree-based algorithm. In arboriculture, the reason to prune tree is because each cut has the potential to change the growth of the tree, no branch should be removed without a reason. Common reasons for pruning are to remove dead branches, to improve form, and to reduce risk. Trees may also be pruned to increase light and air penetration to the inside of the tree’s crown or to the landscape below.

In machine learning, it is to avoid the overfitting, to make a balance between over-fitting and under-fitting and boost the generalization ability. The important step of tree pruning is to define a criterion be used to determine the correct final tree size using one of the following methods:

  1. Use a distinct dataset from the training set (called validation set), to evaluate the effect of post-pruning nodes from the tree.
  2. Build the tree by using the training set, then apply a statistical test to estimate whether pruning or expanding a particular node is likely to produce an improvement beyond the training set.
    • Error estimation
    • Significance testing (e.g., Chi-square test)
  3. Minimum Description Length principle : Use an explicit measure of the complexity for encoding the training set and the decision tree, stopping growth of the tree when this encoding size (size(tree) + size(misclassifications(tree)) is minimized.

When the height of a decision tree is limited to 1, i.e., it takes only one test to make every prediction, the tree is called a decision stump. While decision trees are nonlinear classifiers in general, decision stumps are a kind of linear classifiers.

Fifty Years of Classification and Regression Trees and the website of Wei-Yin Loh helps much understand the decision tree. Multivariate Adaptive Regression Splines(MARS) is the boosting ensemble methods for decision tree algorithms. Recursive partition is a recursive way to construct decision tree.

Random Forest

Decision Trees do not generalize to new variations demonstrates some theoretical limitations of decision trees. And they can be seriously hurt by the curse of dimensionality in a sense that is a bit different from other nonparametric statistical methods, but most importantly, that they cannot generalize to variations not seen in the training set. This is because a decision tree creates a partition of the input space and needs at least one example in each of the regions associated with a leaf to make a sensible prediction in that region. A better understanding of the fundamental reasons for this limitation suggests that one should use forests or even deeper architectures instead of trees, which provide a form of distributed representation and can generalize to variations not encountered in the training data.

Random forests (Breiman, 2001) is a substantial modification of bagging that builds a large collection of de-correlated trees, and then averages them.

On many problems the performance of random forests is very similar to boosting, and they are simpler to train and tune.

  • For $t=1, 2, \dots, T$:
    • Draw a bootstrap sample $Z^{\ast}$ of size $N$ from the training data.
    • Grow a random-forest tree $T_t$ to the bootstrapped data, by recursively repeating the following steps for each terminal node of the tree, until the minimum node size $n_{min}$ is reached.
      • Select $m$ variables at random from the $p$ variables.
      • Pick the best variable/split-point among the $m$.
      • Split the node into two daughter nodes.
  • Vote for classification and average for regression.

Ensemble methods

There are many competing techniques for solving the problem, and each technique is characterized by choices and meta-parameters: when this flexibility is taken into account, one easily ends up with a very large number of possible models for a given task.

Bagging

Bagging, short for 'bootstrap aggregating', is a simple but highly effective ensemble method that creates diverse models on different random bootstrap samples of the original data set. Random forest is the application of bagging to decision tree algorithms.

The basic motivation of parallel ensemble methods is to exploit the independence between the base learners, since the error can be reduced dramatically by combining independent base learners. Bagging adopts the most popular strategies for aggregating the outputs of the base learners, that is, voting for classification and averaging for regression.

  • Draw bootstrap samples $B_1, B_2, \dots, B_n$ independently from the original training data set for base learners;
  • Train the $i$th base learner $F_i$ at the ${B}_{i}$;
  • Vote for classification and average for regression.

It is a sample-based ensemble method.

There is an alternative of bagging called combining ensemble method. It trains a linear combination of learner: $$F = \sum_{i=1}^{n} w_i F_i$$ where the weights $w_i\geq 0, \sum_{i=1}^{n} w_i =1$. The weights $w={w_i}{i=1}^{n}$ are solved by minimizing the ensemble error $$ w = \arg\min{w}\sum_{k}^{K}(F(x_k)-y_k)^{2} $$ if the training data set ${x_k, y_k}_{k=1}^{K}$ is given.

Random Subspace Methods

Abstract: "Much of previous attention on decision trees focuses on the splitting criteria and optimization of tree sizes. The dilemma between overfitting and achieving maximum accuracy is seldom resolved. A method to construct a decision tree based classifier is proposed that maintains highest accuracy on training data and improves on generalization accuracy as it grows in complexity. The classifier consists of multiple trees constructed systematically by pseudorandomly selecting subsets of components of the feature vector, that is, trees constructed in randomly chosen subspaces. The subspace method is compared to single-tree classifiers and other forest construction methods by experiments on publicly available datasets, where the method's superiority is demonstrated. We also discuss independence between trees in a forest and relate that to the combined classification accuracy."

Boosting

The term boosting refers to a family of algorithms that are able to convert weak learners to strong learners. It is kind of similar to the "trial and error" scheme: if we know that the learners perform worse at some given data set $S$, the learner may pay more attention to the data drawn from $S$. For the regression problem, of which the output results are continuous, it progressively reduce the error by trial. In another word, we will reduce the error at each iteration.

AdaBoost

AdaBoost is a boosting methods for supervised classification algorithms, so that the labeled data set is given in the form $D={ (x_i, \mathrm{y}i)}{i=1}^{N}$. AdaBoost is to change the distribution of training data and learn from the shuffled data. It is an iterative trial-and-error in some sense.

  • Input $D={ (x_i, \mathrm{y}i)}{i=1}^{N}$ where $x\in \mathcal X$ and $\mathrm{y}\in {+1, -1}$.
  • Initialize the observation weights ${w}_i=\frac{1}{N}, i=1, 2, \dots, N$.
  • For $t = 1, 2, \dots, T$:
    • Fit a classifier $G_t(x)$ to the training data using weights $w_i$.
    • Compute $$err_{t}=\frac{\sum_{i=1}^{N}w_i \mathbb{I}(G_t(x_i) \not= \mathrm{y}i)}{\sum{i=1}^{N} w_i}.$$
    • Compute $\alpha_t = \log(\frac{1-err_t}{err_t})$.
    • Set $w_i\leftarrow w_i\exp[-\alpha_t(\mathrm{y}_i G_t(x_i))], i=1,2,\dots, N$ and renormalize.
  • Output $G(x)=sign[\sum_{t=1}^{T}\alpha_{t}G_t(x)]$.

The indicator function $\mathbb{I}(x\neq y)$ is defined as $$ \mathbb{I}(x\neq y)= \begin{cases} 1, \text{if $x\neq y$} \ 0, \text{otherwise}. \end{cases} $$

Real AdaBoost

In AdaBoost, the error is binary- it is 0 if the classification is right otherwise it is 1. It is not precise for some setting. The output of decision trees is a class probability estimate $p(x) = P(y=1 | x)$, the probability that ${x}$ is in the positive class

  • Input $D={ (x_i, \mathrm{y}i)}{i=1}^{N}$ where $x\in \mathcal X$ and $y\in {+1, -1}$.
  • Initialize the observation weights ${w}_i=\frac{1}{N}, i=1, 2, \dots, N$;
  • For $m = 1, 2, \dots, M$:
    • Fit a classifier $G_m(x)$ to obtain a class probability estimate $p_m(x)=\hat{P}_{w}(y=1\mid x)\in [0, 1]$, using weights $w_i$.
    • Compute $f_m(x)\leftarrow \frac{1}{2}\log{p_m(x)/(1-p_m(x))}\in\mathbb{R}$.
    • Set $w_i\leftarrow w_i\exp[-y_if_m(x_i)], i=1,2,\dots, N$ and renormalize so that $\sum_{i=1}w_i =1$.
  • Output $G(x)=sign[\sum_{t=1}^{M}\alpha_{t}G_m(x)]$.

Gentle AdaBoost

  • Input $D={ (x_i, \mathrm{y}i)}{i=1}^{N}$ where $x\in \mathcal X$ and $y\in {+1, -1}$.
  • Initialize the observation weights ${w}_i=\frac{1}{N}, i=1, 2, \dots, N, F(x)=0$;
  • For $m = 1, 2, \dots, M$:
    • Fit a classifier $f_m(x)$ by weighted least-squares of $\mathrm{y}_i$ to $x_i$ with weights $w_i$.
    • Update $F(x)\leftarrow F(x)+f_m (x)$.
    • UPdate $w_i \leftarrow w_i \exp(-\mathrm{y}_i f_m (x_i))$ and renormalize.
  • Output the classifier $sign[F(x)]=sign[\sum_{t=1}^{M}\alpha_{t}f_m(x)]$.

LogitBoost

Given a training data set ${{\mathrm{X}i, y_i}}{i=1}^{N}$, where $\mathrm{X}i\in\mathbb{R}^p$ is the feature and $y_i\in{1, 2, \dots, K}$ is the desired categorical label. The classifier $F$ learned from data is a function $$ F:\mathbb{R}^P\to y \ \quad X_i \mapsto y_i. $$ And the function $F$ is usually in the additive model $F(x)=\sum{m=1}^{M}h(x\mid {\theta}_m)$.

where $r_{i, k}=1$ if $y_i =k$ otherwise 0.

  • LogitBoost used first and second derivatives to construct the trees;
  • LogitBoost was believed to have numerical instability problems.

Bonsai Boosted Decision Tree

bonsai BDT (BBDT):

  1. $\fbox{discretizes}$ input variables before training which ensures a fast and robust implementation
  2. converts decision trees to n-dimentional table to store
  3. prediction operation takes one reading from this table

The first step of preprocessing data limits where the splits of the data can be made and, in effect, permits the grower of the tree to control and shape its growth; thus, we are calling this a bonsai BDT (BBDT). The discretization works by enforcing that the smallest keep interval that can be created when training the BBDT is: $$\Delta x_{min} > \delta_x \forall x,,\text{on all leaves}$$ where $\delta_x=\min {|x_i-x_j|: x_i, x_j\in x_{discrete}}$.

Gradient Boosting Decision Tree

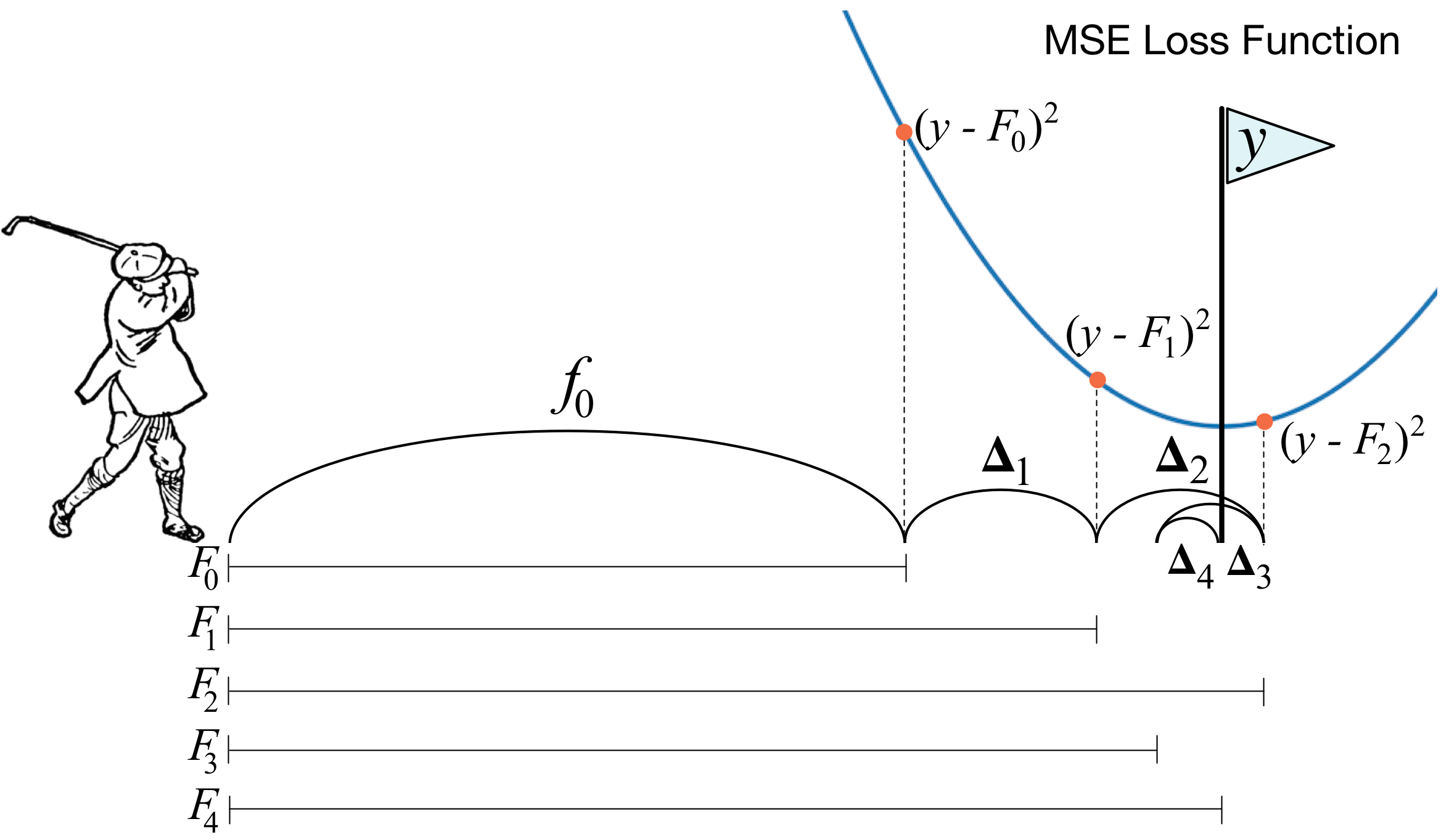
One of the frequently asked questions is What's the basic idea behind gradient boosting? and the answer from [https://explained.ai/gradient-boosting/faq.html] is the best one I know:

Instead of creating a single powerful model, boosting combines multiple simple models into a single composite model. The idea is that, as we introduce more and more simple models, the overall model becomes stronger and stronger. In boosting terminology, the simple models are called weak models or weak learners. To improve its predictions, gradient boosting looks at the difference between its current approximation,$\hat{y}$ , and the known correct target vector ${y}$, which is called the residual, $y-\hat{y}$. It then trains a weak model that maps feature vector ${x}$ to that residual vector. Adding a residual predicted by a weak model to an existing model's approximation nudges the model towards the correct target. Adding lots of these nudges, improves the overall models approximation.

Gradient Boosting

It is the first solution to the question that if weak learner is equivalent to strong learner.

We may consider the generalized additive model, i.e.,

$$ \hat{y}i = \sum{k=1}^{K} f_k(x_i) $$

where ${f_k}_{k=1}^{K}$ is regression decision tree rather than polynomial. The objective function is given by

$$ obj = \underbrace{\sum_{i=1}^{n} L(y_i,\hat{y}i)}{\text{error term} } + \underbrace{\sum_{k=1}^{K} \Omega(f_k)}_{regularazation} $$

where $\sum_{k=1}^{K} \Omega(f_k)$ is the regular term.

The additive training is to train the regression tree sequentially. The objective function of the $t$th regression tree is defined as

$$ obj^{(t)} = \sum_{i=1}^{n} L(y_i,\hat{y}^{(t)}i) + \sum{k=1}^{t} \Omega(f_k) \ = \sum_{i=1}^{n} L(y_i,\hat{y}^{(t-1)}_i + f_t(x_i)) + \Omega(f_t) + C $$

where $C=\sum_{k=1}^{t-1} \Omega(f_k)$.

Particularly, we take $L(x,y)=(x-y)^2$, and the objective function is given by

$$ obj^{(t)} = \sum_{i=1}^{n} [y_i - (\hat{y}^{(t-1)}i + f_t(x_i))]^2 + \Omega(f_t) + C \ = \sum{i=1}^{n} [-2(y_i - \hat{y}^{(t-1)}_i) f_t(x_i) + f_t^2(x_i) ] + \Omega(f_t) + C^{\prime} $$

where $C^{\prime}=\sum_{i=1}^{n} (y_i - \hat{y}^{(t-1)}i)^2 + \sum{k=1}^{t-1} \Omega(f_k)$.

If there is no regular term $\sum_{k=1}^{t} \Omega(f_k)$, the problem is simplified to $$\arg\min_{f_{t}}\sum_{i=1}^{n} [-2(y_i - \hat{y}^{(t-1)}_i) f_t(x_i) + f_t^2(x_i) ]\implies f_t(x_i) = (y_i - \hat{y}^{(t-1)}_i) $$ where $i\in {1,\cdots, n}$ and $(y_i - \hat{y}^{(t-1)}i)=-\frac{1}{2} {[\frac{\partial L(\mathrm{y}i, f(x_i))}{\partial f(x_i)}]}{f=f{t-1}}$.

Boosting for Regression Tree

  • Input training data set ${(x_i, \mathrm{y}_i)\mid i=1, \cdots, n}, x_i\in\mathcal x\subset\mathbb{R}^n, y_i\in\mathcal Y\subset\mathbb R$.
  • Initialize $f_0(x)=0$.
  • For $t = 1, 2, \dots, T$:
    • For $i = 1, 2,\dots , n$ compute the residuals $$r_{i,t}=y_i-f_{t-1}(x_i)=y_i - \hat{y}_i^{t-1}.$$
    • Fit a regression tree to the targets $r_{i,t}$ giving terminal regions $$R_{j,m}, j = 1, 2,\dots , J_m. $$
    • For $j = 1, 2,\dots , J_m$ compute $$\gamma_{j,t}=\arg\min_{\gamma}\sum_{x_i\in R_{j,m}}{L(\mathrm{d}i, f{t-1}(x_i)+\gamma)}. $$
    • Update $f_t = f_{t-1}+ \nu{\sum}{j=1}^{J_m}{\gamma}{j, t} \mathbb{I}(x\in R_{j, m}),\nu\in(0, 1)$.
  • Output $f_T(x)$.

For general loss function, it is more common that $(y_i - \hat{y}^{(t-1)}i) \not=-\frac{1}{2} {[\frac{\partial L(\mathrm{y}i, f(x_i))}{\partial f(x_i)}]}{f=f{t-1}}$.

Gradeint Boosting for Regression Tree

  • Input training data set ${(x_i, \mathrm{y}_i)\mid i=1, \cdots, n}, x_i\in\mathcal x\subset\mathbb{R}^n, y_i\in\mathcal Y\subset\mathbb R$.
  • Initialize $f_0(x)=\arg\min_{\gamma} L(\mathrm{y}_i,\gamma)$.
  • For $t = 1, 2, \dots, T$:
    • For $i = 1, 2,\dots , n$ compute $$r_{i,t}=-{[\frac{\partial L(\mathrm{y}i, f(x_i))}{\partial f(x_i)}]}{f=f_{t-1}}.$$
    • Fit a regression tree to the targets $r_{i,t}$ giving terminal regions $$R_{j,m}, j = 1, 2,\dots , J_m. $$
    • For $j = 1, 2,\dots , J_m$ compute $$\gamma_{j,t}=\arg\min_{\gamma}\sum_{x_i\in R_{j,m}}{L(\mathrm{d}i, f{t-1}(x_i)+\gamma)}. $$
    • Update $f_t = f_{t-1}+ \nu{\sum}{j=1}^{J_m}{\gamma}{j, t} \mathbb{I}(x\in R_{j, m}),\nu\in(0, 1)$.
  • Output $f_T(x)$.

An important part of gradient boosting method is regularization by shrinkage which consists in modifying the update rule as follows: $$ f_{t} =f_{t-1}+\nu \underbrace{ \sum_{j = 1}^{J_{m}} \gamma_{j, t} \mathbb{I}(x\in R_{j, m}) }{ \text{ to fit the gradient} }, \ \approx f{t-1} + \nu \underbrace{ {\sum}{i=1}^{n} -{[\frac{\partial L(\mathrm{y}i, f(x_i))}{\partial f(x_i)}]}{f=f{t-1}} }_{ \text{fitted by a regression tree} }, \nu\in(0,1). $$

Note that the incremental tree is approximate to the negative gradient of the loss function, i.e., $$\fbox{ $\sum_{j=1}^{J_m} \gamma_{j, t} \mathbb{I}(x\in R_{j, m}) \approx {\sum}{i=1}^{n} -{[\frac{\partial L(\mathrm{y}i, f(x_i))}{\partial f(x_i)}]}{f=f{t-1}}$ }$$ where $J_m$ is the number of the terminal regions and ${n}$ is the number of training samples/data.

AdaBoost is related with so-called exponential loss $\exp(-{y_i}p(x_i))$ where $x_i\in\mathbb{R}^p, y_i\in{-1, +1}, p(\cdot)$ is the input features, labels and prediction function, respectively. And the weight is update via the following formula: $$w_i\leftarrow w_i\exp[-y_ip(x_i)], i=1,2,\dots, N.$$

The gradient-boosting algorithm is general in that it only requires the analyst specify a loss function and its gradient. When the labels are multivariate, Alex Rogozhnikova et al define a more general expression of the AdaBoost criteria $$w_i\leftarrow w_i\exp[-y_i\sum_{j}a_{ij}p(x_j)], i=1,2,\dots, N,$$

where $a_{ij}$ are the elements of some square matrix ${A}$. For the case where A is the identity matrix, the AdaBoost weighting procedure is recovered. Other choices of ${A}$ will induce non-local effects, e.g., consider the sparse matrix $A_{knn}$ given by $$a_{ij}^{knn}= \begin{cases} 1, & \text{$j \in knn(i)$; events ${i}$ and ${j}$ belong to the same class} \ 0, & \text{otherwise}. \end{cases}$$

A general gradient descent “boosting” paradigm is developed for additive expansions based on any fitting criterion. It is not only for the decision tree.

Accelerated Gradient Boosting

The difficulty in accelerating GBM lies in the fact that weak (inexact) learners are commonly used, and therefore the errors can accumulate in the momentum term. To overcome it, we design a "corrected pseudo residual" and fit best weak learner to this corrected pseudo residual, in order to perform the z-update. Thus, we are able to derive novel computational guarantees for AGBM. This is the first GBM type of algorithm with theoretically-justified accelerated convergence rate.

  • Initialize $f_0(x)=g_0(x)=0$;
  • For $m = 1, 2, \dots, M$:
    • Compute a linear combination of ${f}$ and ${h}$: $g^{m}(x)=(1-{\theta}_m) f^m(x) + {\theta}_m h^m(x)$ and ${\theta}_m=\frac{2}{m+2}$
    • For $i = 1, 2,\dots , n$ compute $$r_{i, m}=-{[\frac{\partial L(\mathrm{y}_i, g^m(x_i))}{\partial g^m(x_i)}]}.$$
    • Find the best weak-learner for pseudo residual: $${\tau}{m,1}=\arg\min{\tau\in \mathcal T}{\sum}{i=1}^{n}(r{i,m}-b_{\tau}(x_i))^2$$
    • Update the model: $f^{m+1}(x)= g^{m}(x) + \eta b_{\tau_{m,1}}$.
    • Update the corrected residual: $$c_{i,m}=\begin{cases} r_{i, m} & \text{if m=0},\ r_{i, m}+\frac{m+1}{m+2}(c_{i, m-1}-b_{\tau_{m,2}}) & \text{otherwise}.\end{cases}$$
    • Find the best weak-learner for the corrected residual: $b_{\tau_{m,2}}=\arg\min_{\tau\in \mathcal T}{\sum}{i=1}^{n}(c{i,m}-b_{\tau}(x_i))^2$.
    • Update the momentum model: $h^{m+1} = h^{m} + \frac{\gamma\eta}{\theta_m} b_{\tau_{m,2}}(x)$.
  • Output $f^{M}(x)$.

xGBoost

In Gradient Boost, we compute and fit a regression a tree to $$ r_{i,t}=-{ [\frac{\partial L(\mathrm{d}i, f(x_i))}{\partial f(x_i)}] }{f=f_{t-1}}. $$ Why not the error $L(\mathrm{d}_i, f(x_i))$ itself? Recall the Taylor expansion $f(x+h) = f(x)+f^{\prime}(x)h + f^{(2)}(x)h^{2}/2!+ \cdots +f^{(n)}(x)h^{(n)}/n!+\cdots$ so that the non-convex error function can be expressed as a polynomial in terms of $h$, which is easier to fit than a general common non-convex function. So that we can implement additive training to boost the supervised algorithm.

In general, we can expand the objective function at $x^{t-1}$ up to the second order

$$ obj^{(t)} = \sum_{i=1}^{n} L[y_i,\hat{y}^{(t-1)}i + f_t(x_i)] + \Omega(f_t) + C \ \simeq \sum{i=1}^{n} \underbrace{ [L(y_i,\hat{y}^{(t-1)}i) + g_i f_t(x_i) + \frac{h_i f_t^2(x_i)}{2}] }{\text{2ed Order Taylor Expansion}} + \Omega(f_t) + C^{\prime} $$

where $\color{red}{ g_i=\partial_{\hat{y}{i}^{(t-1)}} L(y_i, \hat{y}{i}^{(t-1)}) }$, $\color{red}{h_i=\partial^2_{\hat{y}{i}^{(t-1)}} L(y_i, \hat{y}{i}^{(t-1)})}$.

After we remove all the constants, the specific objective at step ${t}$ becomes $$ obj^{(t)}\approx \sum_{i=1}^{n} [L(y_i,\hat{y}^{(t-1)}_i) + g_i f_t(x_i) + \frac{h_i f_t^2(x_i)}{2}] + \Omega(f_t) $$

One important advantage of this definition is that the value of the objective function only depends on $g_i$ and $h_i$. This is how XGBoost supports custom loss functions.

In order to define the complexity of the tree $\Omega(f)$, let us first refine the definition of the tree $f(x)$ as $$ f_t(x)= w_{q(x)}={\sum}{i=1}^{T} w{i}\mathbb{I} ({q(x)=i}),\ w\in\mathbb{R}^{T}, q:\mathbb{R}^d\Rightarrow {1,2,\dots, T}. $$

Here ${w}$ is the vector of scores on leaves, ${q}$ is a function assigning each data point to the corresponding leaf, and ${T}$ is the number of leaves. In XGBoost, we define the complexity as $$ \Omega(f)=\gamma T + \frac{1}{2}\lambda \sum_{i=1}^{T} {w}_i^2. $$

After re-formulating the tree model, we can write the objective value with the ${t}$-th tree as: $$ obj^{(t)} = \sum_{i=1}^{n}[g_i w_{q(x_i)}+\frac{1}{2} h_i w_{q(x_i)}^2 + \gamma T+\frac{1}{2}\lambda \sum_{i=1}^{n}w_i^2] \=\sum_{j=1}^{T}[(\sum_{i\in I_{j}}g_i)w_j+\frac{1}{2}(\sum_{i\in I_{j}}h_i + \lambda)w_j^2]+\gamma T $$ where $I_j={i\mid q(x_i)=j}$ is the set of indices of data points assigned to the $j$-th leaf. We could further compress the expression by defining $G_j=\sum_{i\in I_j} g_i$ and $H_j=\sum_{i\in I_j} h_i$: $$ obj^{(t)} = \sum_{j=1}^{T}[(G_j w_j+\frac{1}{2}(H_j +\lambda)w_j^2]+\gamma T. $$

In this equation, $w_j$ are independent with respect to each other, the form $G_j w_j + \frac{1}{2}(H_j+\lambda)w^2_j$ is quadratic and the best $w_j$ for a given structure $q(x)$ and the best objective reduction we can get is:

$$ w_j^{\ast} =-(H_j+\lambda )^{-1}G_j,\\ obj^{\ast} =\frac{1}{2}\sum_{j=1}^{T} -(H_j+\lambda )^{-1}G_j^2+\gamma T. $$

Another key of xGBoost is how to a construct a tree fast and painlessly. We will try to optimize one level of the tree at a time. Specifically we try to split a leaf into two leaves, and the score it gains is $$ Gain = \frac{1}{2} \left[\underbrace{\frac{G_L^2}{H_L+\lambda}}{\text{from left leaf}} + \underbrace{\frac{G_R^2}{H_R+\lambda}}{\text{from the right leaf}}-\underbrace{\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}}_{\text{from the original leaf} } \right] - \gamma $$

This formula can be decomposed as 1) the score on the new left leaf 2) the score on the new right leaf 3) The score on the original leaf 4) regularization on the additional leaf. We can see an important fact here: if the gain is smaller than $\gamma$, we would do better not to add that branch. This is exactly the pruning techniques in tree based models! By using the principles of supervised learning, we can naturally come up with the reason these techniques work.

Other features include:
  • row sample;
  • column sample;
  • shrinkages.

LightGBM

LightGBM is a gradient boosting framework that uses tree based learning algorithms. It is designed to be distributed and efficient with the following advantages:

  • Faster training speed and higher efficiency.
  • Lower memory usage.
  • Better accuracy.
  • Support of parallel and GPU learning.
  • Capable of handling large-scale data.

lightGBM

A major reason is that for each feature, they need to scan all the data instances to estimate the information gain of all possible split points, which is very time consuming. To tackle this problem, the authors of lightGBM propose two novel techniques: Gradient-based One-Side Sampling (GOSS) and Exclusive Feature Bundling (EFB).

Leaf-wise learning is to split a leaf(with max delta loss) into 2 leaves rather than split leaves in one level into 2 leaves.

And it limits the depth of the tree in order to avoid over-fitting.

Histogram is an un-normalized empirical cumulative distribution function, where the continuous features (in flow point data structure) is split into ${k}$ buckets by threahold values such as if $x\in [0, 2)$ then ${x}$ will be split into bucket 1. It really reduces the complexity to store the data and compute the impurities based on the distribution of features.

Optimization in parallel learning

A Communication-Efficient Parallel Algorithm for Decision Tree

CatBoost

CatBoost is an algorithm for gradient boosting on decision trees. Developed by Yandex researchers and engineers, it is the successor of the MatrixNet algorithm that is widely used within the company for ranking tasks, forecasting and making recommendations. It is universal and can be applied across a wide range of areas and to a variety of problems such as search, recommendation systems, personal assistant, self-driving cars, weather prediction and many other tasks. It is in open-source and can be used by anyone now.

CatBoost is based on gradient boosted decision trees. During training, a set of decision trees is built consecutively. Each successive tree is built with reduced loss compared to the previous trees.

The number of trees is controlled by the starting parameters. To prevent over-fitting, use the over-fitting detector. When it is triggered, trees stop being built.

Before learning, the possible values of objects are divided into disjoint ranges ($\color{red}{\fbox{buckets}}$) delimited by the threshold values ($\color{red}{\fbox{splits}}$). The size of the quantization (the number of splits) is determined by the starting parameters (separately for numerical features and numbers obtained as a result of converting categorical features into numerical features).

Quantization is also used to split the label values when working with categorical features. А random subset of the dataset is used for this purpose on large datasets.

Two critical algorithmic advances introduced in CatBoost are the implementation of ordered boosting, a permutation-driven alternative to the classic algorithm, and an innovative algorithm for processing categorical features. Both techniques were created to fight a prediction shift caused by a special kind of target leakage present in all currently existing implementations of gradient boosting algorithms.

The most widely used technique which is usually applied to low-cardinality categorical features is one-hot encoding; another way to deal with categorical features is to compute some statistics using the label values of the examples. Namely, assume that we are given a dataset of observations $D = {(\mathrm{X}i, \mathrm{Y}i)\mid i=1,2,\cdots, n}$, where $\mathrm{X}i = (x{i,1}, x{i, 2}, \cdots, x{i,m})$ is a vector of ${m}$ features, some numerical, some categorical, and $\mathrm{Y}i\in\mathbb{R}$ is a label value. The simplest way is to substitute the category with the average label value on the whole train dataset. So, $x{i;k}$ is substituted with $\frac{\sum_{j=1}^n [x_{j;k}=x_{i;k}]\cdot \mathrm{Y}j}{\sum{j=1}^n [x_{j;k}=x_{i;k}]}$; where $[\cdot]$ denotes Iverson brackets, i.e., $[x_{j;k} = x_{i;k}]$ equals 1 if $x_{j;k} = x_{i;k}$ and 0 otherwise. This procedure, obviously, leads to overfitting.

CatBoost uses a more efficient strategy which reduces overfitting and allows to use the whole dataset for training. Namely, we perform a random permutation of the dataset and for each example we compute average label value for the example with the same category value placed before the given one in the permutation. Let $\sigma=(\sigma_1, \cdots, \sigma_n)$ be the permutation, then $x_{\sigma_p;k}$ is substituted with $$\frac{\sum_{j=1}^{p-1} [x_{\sigma_j; k}=x_{\sigma_p;k}]\cdot \mathrm{Y}{\sigma_j} + a\cdot P}{\sum{j=1}^{p-1} [x_{\sigma_j; k}=x_{\sigma_p;k}]}$$

where we also add a prior value ${P}$ and a parameter $a > 0$, which is the weight of the prior.

THREE

Andrey Gulin

More: TencentBoost, ThunderGBM and Beyond

There are more gradient boost tree algorithms such as ThubderGBM, TencentBoost, GBDT on angle and H2o.

Gradient boosting tree (GBT), a widely used machine learning algorithm, achieves state-of-the-art performance in academia, industry, and data analytics competitions. Although existing scalable systems which implement GBT, such as XGBoost and MLlib, perform well for data sets with medium-dimensional features, they can suffer performance degradation for many industrial applications where the trained data sets contain high dimensional features. The performance degradation derives from their inefficient mechanisms for model aggregation-either map-reduce or all-reduce. To address this high-dimensional problem, we propose a scalable execution plan using the parameter server architecture to facilitate the model aggregation. Further, we introduce a sparse-pull method and an efficient index structure to increase the processing speed. We implement a GBT system, namely TencentBoost, in the production cluster of Tencent Inc. The empirical results show that our system is 2-20× faster than existing platforms.

Optimization and Boosting

What is the alternative of gradient descent in order to combine ADMM as an operator splitting methods for numerical optimization and Boosting such as gradient boosting/extreme gradient boosting? Can we do leaves splitting and optimization in the same stage?

The core transfer is how to change the original optimization to one linearly constrained convex optimization so that it adjusts to ADMM:

$$ \arg\min_{f_{t}\in\mathcal F}\sum_{i=1}^{n} L[y_i,\hat{y}^{(t-1)}i + f_t(x_i)] + \gamma T +\frac{\lambda}{2}{\sum}{i=1}^{T}w_i^2 \iff \fbox{???} \quad ? $$ where $f_t(x)={\sum}_{i=1}^{T}w_i\mathbb{I}(q(x)=i)$.

It seems attractive to me to understand the analogy between $\fbox{operator splitting in ADMM}$ and $\fbox{leaves splitting in Decision Tree}$.

To be more general, how to connect the numerical optimization methods such as fixed pointed iteration methods and the boosting algorithms? Is it possible to combine $\fbox{Anderson Acceleration}$ and $\fbox{Gradinet Boosting}$ ?

Boosting Optimziation
AdaBoost Coordinate-wise Descent
Stochastic Gradient Boost Stochastic Gradient Descent
Gradient Boost Gradient Descent
Accelerated Gradient Boosting Accelerated Gradient Descent
xGBoost Newton's Methods
? Mirror Gradient Descent
? ADMM

AdaBoost stepwise minimizes a function $$L(G_t)=\sum_{n=1}^N \exp(-\mathrm{y}_n G_t(x_n))$$ The gradient of $L(G_t)$ gives the example weights used for AdaBoost: $$\frac{\partial L(G_t)}{\partial G_t(x_n)}=-\mathrm{y}_n\exp(-\mathrm{y}_nG_t(x_n)).$$

Compared with entropic descent method, in each iteration of AdaBoost: $$w_i\leftarrow w_i\exp[-\alpha_t(\mathrm{y}i G_t(x_i))]>0, i=1,2,\dots, N, \sum{n=1}^{N}w_n=1.$$

$\color{red}{Note}$: given the input feature $x_i$, the label $\mathrm y_i$ is a fixed constant and the model is modified with the training data set and the distribution $(D, w)$ i.e., ${(x_i, y_i, w_i)\mid i=1,2,\cdots, N}$.

Another interesting question is how to boost the composite/multiplicative models rather than the additive model?

The Generic Leveraging Algorithm

Let us assume the loss function $G(f, D)$ has the following additive form $$G(f, D)=\sum_{n=1}^{N} g(f(x_n), y_n),$$ and we would like to solve the optimization problem $$\min_{f\in\mathcal F}G(f, D)=\min_{w}\sum_{n=1}^{N} g(f_w(x_n), y_n).$$ And $g^{\prime}(f_w(x_n), y_n))=\frac{\partial g(f_w(x_n), y_n)}{\partial f_w(x_n)}$ for $n=1,2,\cdots, N$.

  • Input $D={ (x_i, y_i)}_{i=1}^{N}$;Loss function $G:\mathbb{R}^n\to\mathbb{R}$ .
  • Initialize the observation weights $f_o=0, d_n^1=g^{\prime}(f_0(x_n), y_n), n=1, 2, \dots, N$.
  • For $t = 1, 2, \dots, T$:
    • Train classifier on ${D, \mathbf d^t}$ and obtain hypothesis $h_t:\mathbb{X}\to\mathbb{Y}$
    • Set $\alpha_t=\arg\min_{\alpha\in\mathbb{R}}G[f_t + \alpha h_t]$
    • Update $f_{t+1} = f_t + {\alpha_t}h_t$ and $d_n^{t+1}=g^{\prime}(f_{t+1}(x_n), y_n), n=1, 2, \dots, N$
  • Output $f_T$.

Here $\mathbf d^t=(d^t_1, d^t_2, \cdots, d^t_N)$ for $t=1,2,\cdots, T$.

$\fbox{Leveraging = Boosting without PAC Boosting property}$

Matrix Multiplicative Weight Algorithms

Matrix Multiplicative Weight can be considered as an ensemble method of optimization methods. The name “multiplicative weights” comes from how we implement the last step: if the weight of the chosen object at step $t$ is $w_t$ before the event, and $G$ represents how well the object did in the event, then we’ll update the weight according to the rule: $$ w_{t+1}=w_{t}(1+G). $$

Matrix Multiplicative Weight

Jeremy wrote a blog on this topic:

In general we have some set $X$ of objects and some set $Y$ of “event outcomes” which can be completely independent. If these sets are finite, we can write down a table M whose rows are objects, whose columns are outcomes, and whose $i,j$ entry $M(i,j)$ is the reward produced by object $x_i$ when the outcome is $y_j$. We will also write this as $M(x, y)$ for object $x$ and outcome $y$. The only assumption we’ll make on the rewards is that the values $M(x, y)$ are bounded by some small constant $B$ (by small I mean $B$ should not require exponentially many bits to write down as compared to the size of $X$). In symbols, $M(x,y) \in [0,B]$. There are minor modifications you can make to the algorithm if you want negative rewards, but for simplicity we will leave that out. Note the table $M$ just exists for analysis, and the algorithm does not know its values. Moreover, while the values in $M$ are static, the choice of outcome $y$ for a given round may be nondeterministic.

The MWUA algorithm randomly chooses an object $x \in X$ in every round, observing the outcome $y \in Y$, and collecting the reward $M(x,y)$ (or losing it as a penalty). The guarantee of the MWUA theorem is that the expected sum of rewards/penalties of MWUA is not much worse than if one had picked the best object (in hindsight) every single round.

Theorem (from Arora et al): The cumulative reward of the MWUA algorithm is, up to constant multiplicative factors, at least the cumulative reward of the best object minus $\log(n)$, where $n$ is the number of objects.

Application

Stacking

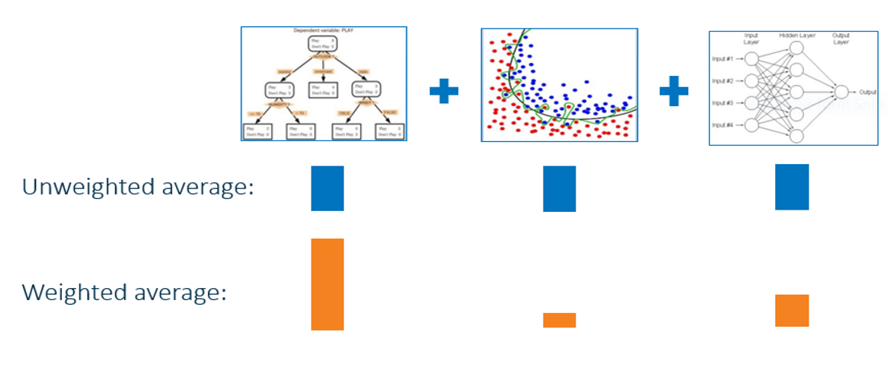
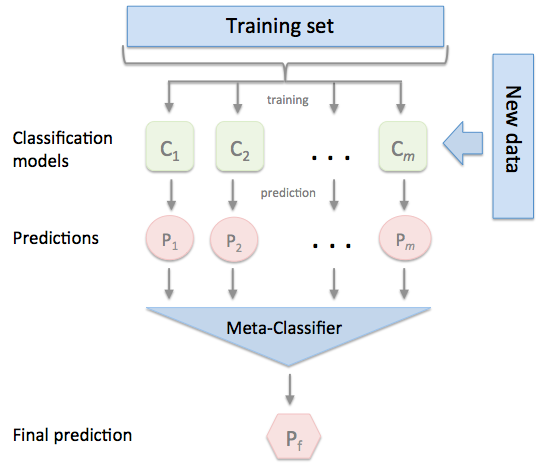
Stacked generalization (or stacking) is a different way of combining multiple models, that introduces the concept of a meta learner. Although an attractive idea, it is less widely used than bagging and boosting. Unlike bagging and boosting, stacking may be (and normally is) used to combine models of different types.

The procedure is as follows:

  1. Split the training set into two disjoint sets.
  2. Train several base learners on the first part.
  3. Test the base learners on the second part.
  4. Using the predictions from 3) as the inputs, and the correct responses as the outputs, train a higher level learner.

Note that steps 1) to 3) are the same as cross-validation, but instead of using a winner-takes-all approach, we train a meta-learner to combine the base learners, possibly non-linearly. It is a little similar with composition of functions in mathematics.

Stacking, Blending and and Stacked Generalization are all the same thing with different names. It is a kind of ensemble learning.

In the sense of stacking, deep neural network is thought as the stacked logistic regression. And Boltzman machine can be stacked in order to construct more expressive model for discrete random variables.

Deep Forest

Other ensemble methods include clustering methods ensemble, dimensionality reduction ensemble, regression ensemble, ranking ensemble.