-
Notifications
You must be signed in to change notification settings - Fork 3
/
rekurzija.html
233 lines (209 loc) · 6.67 KB
/
rekurzija.html
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
<!DOCTYPE html>
<html lang="sl">
<head>
<meta charset="utf-8" />
<meta content="O računalniški rekurziji, povezavi s fraktali, Python primer izračuna Fibonaccijevih števil rekurzivno in iterativno, zakaj rekurzija, ..." name="description" />
<title>Rekurzija</title>
<link href="../remark-style.css" rel="stylesheet" type="text/css">
<style>
</style>
</head>
<body>
<noscript>Če <b>omogočite JavaScript</b>, ta stran postane poučna prezentacija.</noscript>
<textarea id="source">
class: center, middle
# Rekurzija
Če hočete razumeti rekurzijo, morate najprej razumeti rekurzijo.
---
## Rekurzija v slikah
.wh100[]
---
.col2[.center[]]
.col2[.center[]]
---
.wh100[]
---
.wh100[]
---
## Definicija
<iframe width="100%" height="300" src="//bos.zrc-sazu.si/cgi/a03.exe?name=sskj_testa&expression=rekurz&hs=1" frameborder="0"></iframe>
Rekurzija je **postopek**, ki je definiran (določen, **opisan**) **sam s sabo**.
.small[Rešitev celotnega problema vključuje rešitev istega problema nad manjšim obsegom podatkov.]
---
# Fraktali
... so [**samopodobni**](https://en.wikipedia.org/wiki/Self-similarity) in **definirani rekurzivno**
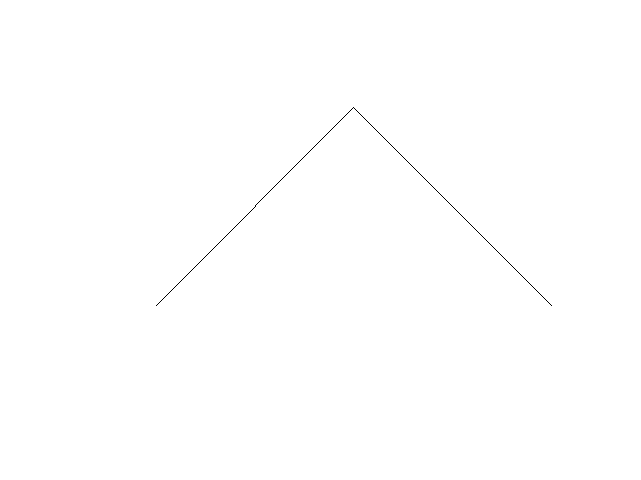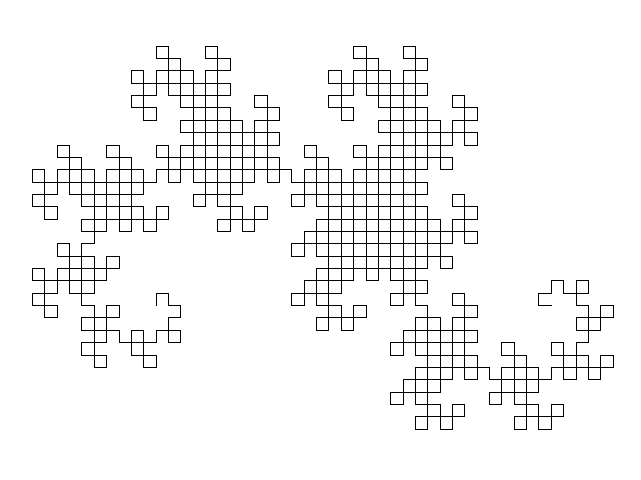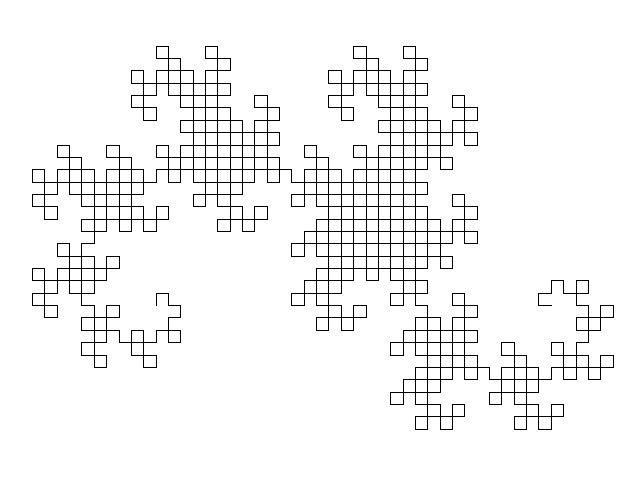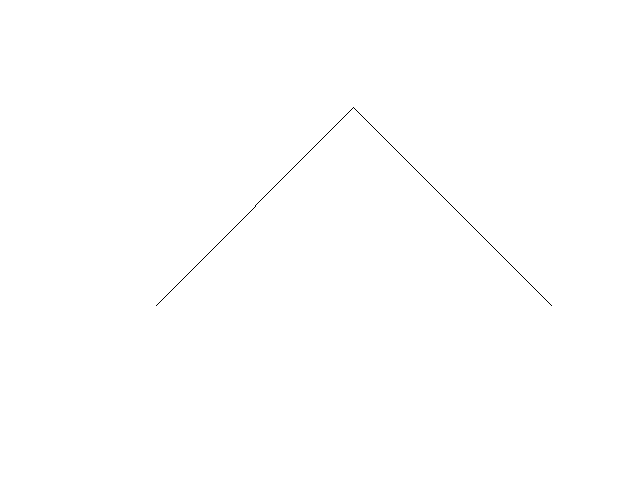
---
## Sierpinski trikotnik
.center[]
---
## Sierpinski trikotnik ...
.center[<img alt="konstrukcija trikotnika Sierpinskega" src="../resources/rekurzija/sierpinski2.png" style="width:50%"/>]
???
Kot da bi imeli funkcijo `narisi_bel_trikotnik(mere_crnega_trikotnika)`.
---
## Cantorjevi krogi
.center[<img alt="Cantorjevi krogi" src="../resources/rekurzija/cantor.png" style="width:70%"/>]
---
## Kochova snežinka
.center[<img alt="Kochova snežinka" src="../resources/rekurzija/koch-snowflake.png" style="width:80%"/>]
---
## Pitagorovo drevo
.center[<img alt="Konstrukcija Pitagorovega drevesa" src="../resources/rekurzija/pythagoras-tree1.png" style="width:100%"/>]
Oblika drevesa odvisna od začetnih parametrov sistema (kotov trikotnika).
---
## Pitagorovo drevo ...

---
## Pitagorovo drevo ...
.center[]
---
## Pitagorovo drevo ...
.center[<iframe width="600" height="400" src="//www.youtube.com/embed/jEmSxcr-rRc?rel=0" frameborder="0" allowfullscreen></iframe>]
---
## Pitagorovo drevo ...
.center[]
---
.wh100[]
---
## Fraktali v naravi...
<img alt="Fraktali v naravi: porečje, strela, romanesco brokoli, praprot, aloe vera, ledene rože, drevesni list" src="../resources/rekurzija/fraktali-v-naravi.png" style="width:100%;height:100%;left:0;top:0;position:absolute;">
---
## Fibonaccijevo zaporedje
Recimo, da imamo zaporedje števil,
<br>
kjer je **vsako naslednje** število **vsota prejšnjih dveh**:
.u[**0**, **1**], 1, 2, 3, 5, 8,
--
13,
--
21,
--
34,
--
55,
--
89, ...
.small[Zanimiva lastnost: vsako število je približno
[1.618](https://www.google.com/search?q=zlati+rez)-krat večje od prejšnjega.]
--
Python koda:
--
```python
def fib(N):
return fib(N-1) + fib(N-2) # ponovimo rekurzivni klic fib()
```
--
Kaj se zgodi?
--
```python
>>> def fib(N):
... return fib(N-1) + fib(N-2)
...
>>> fib(5)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<stdin>", line 2, in fib
File "<stdin>", line 2, in fib
... # par sto ali tisoč vrstic
File "<stdin>", line 2, in fib
File "<stdin>", line 2, in fib
RuntimeError: maximum recursion depth exceeded
```
---
class: bg-black
.center[]
---
## Ustavitveni pogoj
Če želimo enkrat priti do rešitve (končati problem), potem očitno
ne moremo nadaljevati v nedogled. Potreben je **ustavitveni pogoj**.
Kdaj v postopku ne uporabimo spet istega postopka ampak se ustavimo?
???
Kdaj?
--
<br><br>
→ Običajno takrat, **ko je problem dovolj majhen** (enostaven).
.small[V primeru prejšnjih trikotnikov, krogov, snežinke in dreves: npr. ko je razdalja neke črte < 1px.]
--
Ustavitveni pogoj najraje definiramo čimprej v funkciji, da ga ne pozabimo.
Najbolje na začetku funkcije, **vsekakor pa vedno pred rekurzivnim klicem**!
.small[(Sicer dobimo `RuntimeError: maximum recursion depth exceeded`...)]
???
Ker gremo drugače vedno spet v rekurzivni klic, namesto da bi rekurzijo zapustili.
---
## Ustavitveni pogoj ...
Fibonaccijevo zaporedje:
.center[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...]<br>
```python
def fib(N):
# ??? kaj manjka tukaj ???
return fib(N-1) + fib(N-2)
```
???
* Kaj manjka v kodi?
* Katera **ključna beseda** je povezavana s 'pogojem'? (`if`)
* Kdaj je **problem dovolj majhen**?
---
## Ustavitveni pogoj ...
Fibonaccijevo zaporedje:
.center[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...]<br>
```python
def fib(N):
if N <= 1: # izhodni pogoj
return N # ne ponovimo rekurzivnega klica, ampak samo vrnemo vrednost N
else:
return fib(N-1) + fib(N-2)
```
--
Kaj se zgodi?
--
```python
>>> def fib(N):
... return N if N <= 1 else fib(N-1) + fib(N-2)
...
>>> fib(5)
5
>>> [fib(i) for i in range(12)]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
```
---
## Zakaj rekurzija
* Veliko problemov lahko rešimo rekurzivno (risanje dreves,
sortiranje/iskanje elementov seznama, parsanje HTML značk; katerikoli problem,
ki ga lahko razgradimo na enake podprobleme).
* Lepša koda.
Vsako kodo z rekurzijo lahko prepišemo v iterativno kodo
(tj. z [_iteracijami_](https://sl.wikipedia.org/wiki/Iteracija), brez rekurzije).
.col2[
Rekurzivna koda:
```python
def fib(N):
if N <= 1:
return N
else:
return fib(N-1) + fib(N-2)
```
]
.col2[
Iterativna koda:
```python
def fib_iter(N):
a, b = 0, 1 # prvi dve števili zaporedja
while N > 0:
N, a, b = N-1, b, a+b
return a
```
]
???
* Zakaj je desna koda iterativna? Kje je rekurzija v desni kodi? V levi?
* Katera koda vam je bolj všeč?
* Katera koda je boljša?
* Nerekurzivna koda je (v tem primeru) **hitrejša** in zasede
**manj pomnilnika**. Ne pa vedno!
--
#.center[Vprašanja?]
</textarea>
<script src="../remark.min.js"></script>
<script src="../remark-script.js"></script>
</body>
</html>